Estimating the effective reproduction number in Belgium with the RKI method¶
Using the Robert Koch Institute method with serial interval of 4.
Every day Bart Mesuere tweets a nice dashboard with current numbers about Covid-19 in Belgium. This was the tweet on Wednesday 20/11/04:
twitter: https://twitter.com/BartMesuere/status/1323881489864548352
It's nice to see that the effective reproduction number ($Re(t)$) is again below one. That means the power of virus is declining and the number of infection will start to lower. This occured first on Tuesday 2020/11/3:
twitter: https://twitter.com/BartMesuere/status/1323519613855059968
I estimated the $Re(t)$ earlier with rt.live model in this notebook. There the $Re(t)$ was still estimated to be above one. Michael Osthege replied with a simulation results with furter improved model:
twitter: https://twitter.com/theCake/status/1323211910481874944
In that estimation, the $Re(t)$ was also not yet heading below one at the end of october.
In this notebook, we will implement a calculation based on the method of the Robert Koch Institute. The method is described and programmed in R in this blog post.
In that blogpost there's a link to a website with estimations for most places in the world The estimation for Belgium is here
According to that calculation, $Re(t)$ is already below zero for some days.
Load libraries and data¶
df_tests = pd.read_csv('https://epistat.sciensano.be/Data/COVID19BE_tests.csv', parse_dates=['DATE'])
df_cases = pd.read_csv('https://epistat.sciensano.be/Data/COVID19BE_CASES_AGESEX.csv', parse_dates=['DATE'])
df_cases
| DATE | PROVINCE | REGION | AGEGROUP | SEX | CASES | |
|---|---|---|---|---|---|---|
| 0 | 2020-03-01 | Antwerpen | Flanders | 40-49 | M | 1 |
| 1 | 2020-03-01 | Brussels | Brussels | 10-19 | F | 1 |
| 2 | 2020-03-01 | Brussels | Brussels | 10-19 | M | 1 |
| 3 | 2020-03-01 | Brussels | Brussels | 20-29 | M | 1 |
| 4 | 2020-03-01 | Brussels | Brussels | 30-39 | F | 1 |
| ... | ... | ... | ... | ... | ... | ... |
| 36279 | NaT | VlaamsBrabant | Flanders | 40-49 | M | 3 |
| 36280 | NaT | VlaamsBrabant | Flanders | 50-59 | M | 1 |
| 36281 | NaT | WestVlaanderen | Flanders | 20-29 | F | 1 |
| 36282 | NaT | WestVlaanderen | Flanders | 50-59 | M | 3 |
| 36283 | NaT | NaN | NaN | NaN | NaN | 1 |
36284 rows × 6 columns
Reformat data into Rtlive format
df_cases_per_day = (df_cases
.dropna(subset=['DATE'])
.assign(region='Belgium')
.groupby(['region', 'DATE'], as_index=False)
.agg(cases=('CASES', 'sum'))
.rename(columns={'DATE':'date'})
.set_index(["region", "date"])
)
What's in our basetable:
| cases | ||
|---|---|---|
| region | date | |
| Belgium | 2020-03-01 | 19 |
| 2020-03-02 | 19 | |
| 2020-03-03 | 34 | |
| 2020-03-04 | 53 | |
| 2020-03-05 | 81 | |
| ... | ... | |
| 2020-11-01 | 2660 | |
| 2020-11-02 | 13345 | |
| 2020-11-03 | 11167 | |
| 2020-11-04 | 4019 | |
| 2020-11-05 | 5 |
250 rows × 1 columns
Let's plot the number of cases in function of the time.
ax = df_cases_per_day.loc['Belgium'].plot(figsize=(18,6))
ax.set(ylabel='Number of cases', title='Number of cases for covid-19 and number of positives in Belgium');
We see that the last days are not yet complete. Let's cut off the last two days of reporting.
Calculate the date two days ago:
datetime.date(2020, 11, 3)
# today_minus_two = datetime.date.today() + relativedelta(days=-2)
today_minus_two = datetime.date(2020, 11, 3) # Fix the day
today_minus_two.strftime("%Y-%m-%d")
'2020-11-03'
Replot the cases:
ax = df_cases_per_day.loc['Belgium'][:today_minus_two].plot(figsize=(18,6))
ax.set(ylabel='Number of cases', title='Number of cases for covid-19 and number of positives in Belgium');
Select the Belgium region:
| cases | |
|---|---|
| date | |
| 2020-03-01 | 19 |
| 2020-03-02 | 19 |
| 2020-03-03 | 34 |
| 2020-03-04 | 53 |
| 2020-03-05 | 81 |
| ... | ... |
| 2020-10-30 | 15185 |
| 2020-10-31 | 6243 |
| 2020-11-01 | 2660 |
| 2020-11-02 | 13345 |
| 2020-11-03 | 11167 |
248 rows × 1 columns
Check the types of the columns:
<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 248 entries, 2020-03-01 to 2020-11-03
Data columns (total 1 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 cases 248 non-null int64
dtypes: int64(1)
memory usage: 3.9 KB
Robert Koch Institute method¶
A basic method to calculate the effective reproduction number is described (among others) in this blogpost. I included the relevant paragraph:
In a recent report (an der Heiden and Hamouda 2020) the RKI described their method for computing R as part of the COVID-19 outbreak as follows (p. 13): For a constant generation time of 4 days, one obtains R as the ratio of new infections in two consecutive time periods each consisting of 4 days. Mathematically, this estimation could be formulated as part of a statistical model:
$$y_{s+4} | y_{s} \sim Po(R \cdot y_{s}), s= 1,2,3,4$$
where $y_{1}, \ldots, y_{4}$ are considered as fixed. From this we obtain
$$\hat{R}{RKI} = \sum$$}^{4} y_{s+4} / \sum_{s=1}^{4} y_{s
Somewhat arbitrary, we denote by $Re(t)$ the above estimate for R when $s=1$ corresponds to time $t-8$, i.e. we assign the obtained value to the last of the 8 values used in the computation.
In Python, we define a lambda function that we apply on a rolling window. Since indexes start from zero, we calculate:
$$\hat{R}{RKI} = \sum$$}^{3} y_{s+4} / \sum_{s=0}^{3} y_{s
| cases | |
|---|---|
| date | |
| 2020-03-01 | NaN |
| 2020-03-02 | NaN |
| 2020-03-03 | NaN |
| 2020-03-04 | NaN |
| 2020-03-05 | NaN |
| ... | ... |
| 2020-10-30 | 1.273703 |
| 2020-10-31 | 0.929291 |
| 2020-11-01 | 0.601838 |
| 2020-11-02 | 0.499806 |
| 2020-11-03 | 0.475685 |
248 rows × 1 columns
The first values are Nan because the window is in the past. If we plot the result, it looks like this:
ax = df.rolling(8).apply(rt).plot(figsize=(16,4), label='Re(t)')
ax.set(ylabel='Re(t)', title='Effective reproduction number estimated with RKI method')
ax.legend(['Re(t)']);
To avoid the spikes due to weekend reporting issue, I first applied a rolling mean on a window of 7 days:
ax = df.rolling(7).mean().rolling(8).apply(rt).plot(figsize=(16,4), label='Re(t)')
ax.set(ylabel='Re(t)', title='Effective reproduction number estimated with RKI method after rolling mean on window of 7 days')
ax.legend(['Re(t)']);
Interactive visualisation in Altair¶
import altair as alt
alt.Chart(df.rolling(7).mean().rolling(8).apply(rt).fillna(0).reset_index()).mark_line().encode(
x=alt.X('date:T'),
y=alt.Y('cases', title='Re(t)'),
tooltip=['date:T', alt.Tooltip('cases', format='.2f')]
).transform_filter(
alt.datum.date > alt.expr.toDate('2020-03-13')
).properties(
width=600,
title='Effective reproduction number in Belgium based on Robert-Koch Institute method'
)
Making the final visualisation in Altair¶
In the interactive Altair figure below, we show the $Re(t)$ for the last 14 days. We reduce the rolling mean window to three to see faster reactions.
#collapse
df_plot = df.rolling(7).mean().rolling(8).apply(rt).fillna(0).reset_index()
last_value = str(df_plot.iloc[-1]['cases'].round(2)) + ' ↓'
first_value = str(df_plot[df_plot['date'] == '2020-10-21'].iloc[0]['cases'].round(2)) # + ' ↑'
today_minus_15 = datetime.datetime.today() + relativedelta(days=-15)
today_minus_15_str = today_minus_15.strftime("%Y-%m-%d")
line = alt.Chart(df_plot).mark_line(point=True).encode(
x=alt.X('date:T', axis=alt.Axis(title='Datum', grid=False)),
y=alt.Y('cases', axis=alt.Axis(title='Re(t)', grid=False, labels=False, titlePadding=40)),
tooltip=['date:T', alt.Tooltip('cases', title='Re(t)', format='.2f')]
).transform_filter(
alt.datum.date > alt.expr.toDate(today_minus_15_str)
).properties(
width=600,
height=100
)
hline = alt.Chart(pd.DataFrame({'cases': [1]})).mark_rule().encode(y='cases')
label_right = alt.Chart(df_plot).mark_text(
align='left', dx=5, dy=-10 , size=15
).encode(
x=alt.X('max(date):T', title=None),
text=alt.value(last_value),
)
label_left = alt.Chart(df_plot).mark_text(
align='right', dx=-5, dy=-40, size=15
).encode(
x=alt.X('min(date):T', title=None),
text=alt.value(first_value),
).transform_filter(
alt.datum.date > alt.expr.toDate(today_minus_15_str)
)
source = alt.Chart(
{"values": [{"text": "Data source: Sciensano"}]}
).mark_text(size=12, align='left', dx=-57).encode(
text="text:N"
)
alt.vconcat(line + label_left + label_right + hline, source).configure(
background='#D9E9F0'
).configure_view(
stroke=None, # Remove box around graph
).configure_axisY(
ticks=False,
grid=False,
domain=False
).configure_axisX(
grid=False,
domain=False
).properties(title={
"text": ['Effective reproduction number for the last 14 days in Belgium'],
"subtitle": [f'Estimation based on the number of cases until {today_minus_two.strftime("%Y-%m-%d")} after example of Robert Koch Institute with serial interval of 4'],
}
)
# .configure_axisY(
# labelPadding=50,
# )
To check the calculation, here are the last for values for the number of cases after applying the mean window of 7:
| cases | |
|---|---|
| date | |
| 2020-10-27 | 16067.571429 |
| 2020-10-28 | 16135.857143 |
| 2020-10-29 | 15744.571429 |
| 2020-10-30 | 15218.000000 |
Those must be added together:
cases 63166.0
dtype: float64
And here are the four values, starting four days ago:
| cases | |
|---|---|
| date | |
| 2020-10-31 | 14459.428571 |
| 2020-11-01 | 14140.428571 |
| 2020-11-02 | 13213.428571 |
| 2020-11-03 | 11641.428571 |
These are added together:
cases 53454.714286
dtype: float64
And now we divide those two sums to get the $Re(t)$ of 2020-11-03:
cases 0.846258
dtype: float64
This matches (as expected) the value in the graph. Let's compare with three other sources:
- Alas it does not match the calculation reported by Bart Mesuere on 2020-11-03 based on the RKI model that reports 0.96:
twitter: https://twitter.com/BartMesuere/status/1323519613855059968
-
Also, the more elaborated model from rtliveglobal is not yet that optimistic. Mind that model rtlive start estimating the $Re(t)$ from the number of tests instead of the number of cases. It might be that other reporting delays are involved.
-
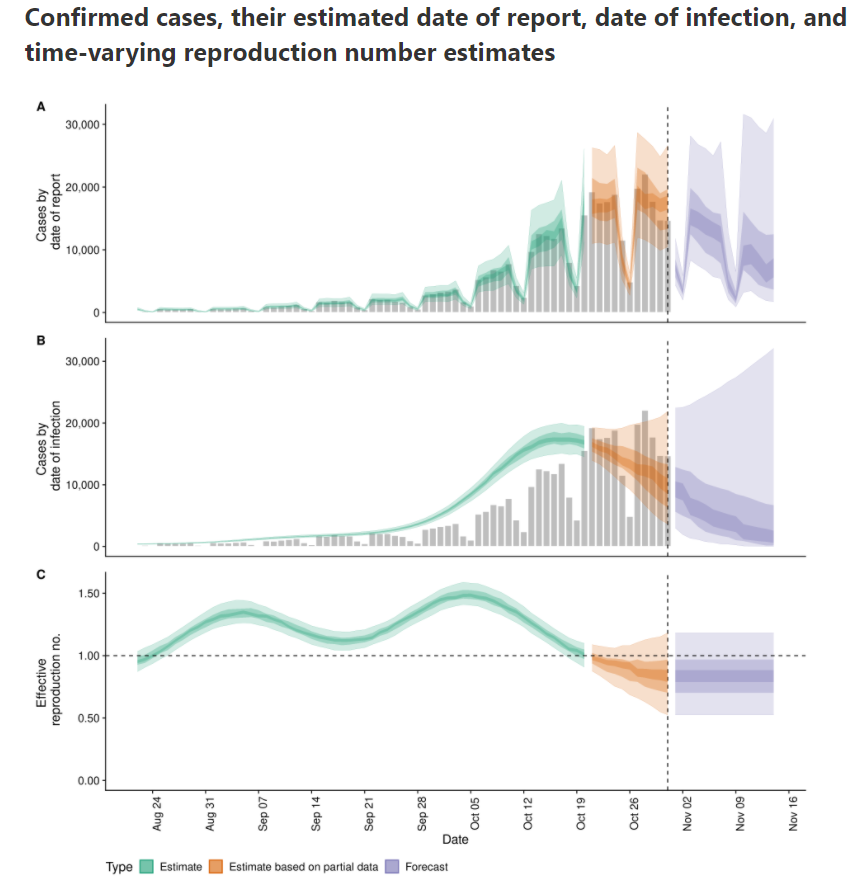
epiforecast.io is already below 1 since beginning of November.
Another possiblity is that I made somewhere a mistake. If you spot it, please let me know.