2020¶
Estimating the effective reproduction number in Belgium with the RKI method
Using the Robert Koch Institute method with serial interval of 4.
Every day Bart Mesuere tweets a nice dashboard with current numbers about Covid-19 in Belgium. This was the tweet on Wednesday 20/11/04:
twitter: https://twitter.com/BartMesuere/status/1323881489864548352
It's nice to see that the effective reproduction number ($Re(t)$) is again below one. That means the power of virus is declining and the number of infection will start to lower. This occured first on Tuesday 2020/11/3:
twitter: https://twitter.com/BartMesuere/status/1323519613855059968
I estimated the $Re(t)$ earlier with rt.live model in this notebook. There the $Re(t)$ was still estimated to be above one. Michael Osthege replied with a simulation results with furter improved model:
twitter: https://twitter.com/theCake/status/1323211910481874944
In that estimation, the $Re(t)$ was also not yet heading below one at the end of october.
In this notebook, we will implement a calculation based on the method of the Robert Koch Institute. The method is described and programmed in R in this blog post.
In that blogpost there's a link to a website with estimations for most places in the world The estimation for Belgium is here
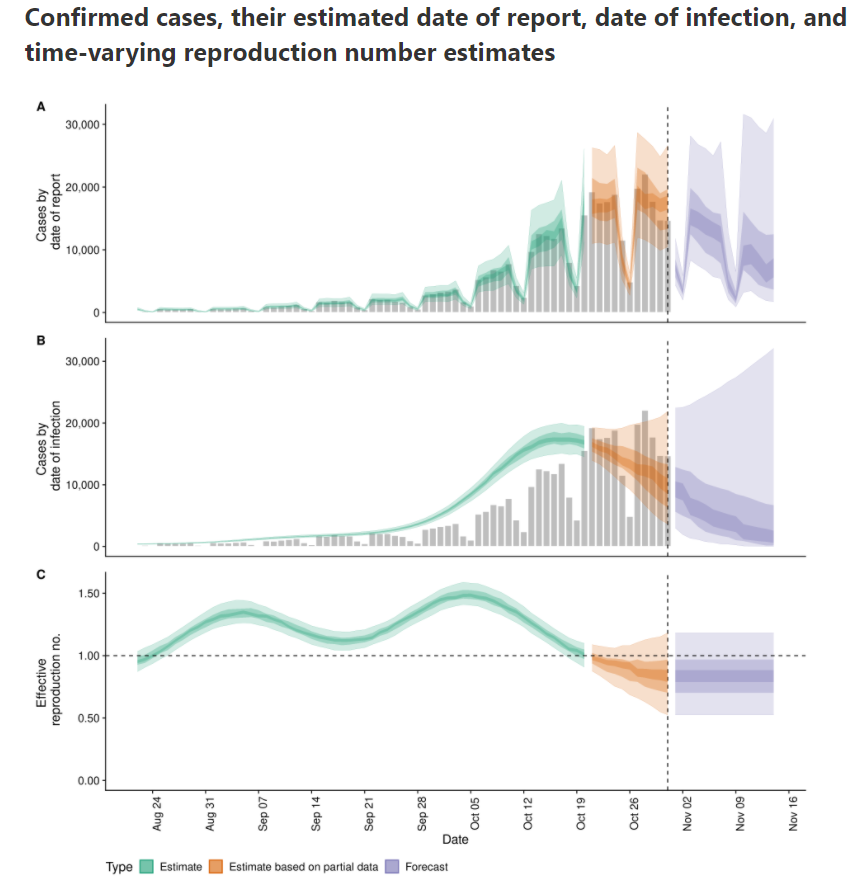
According to that calculation, $Re(t)$ is already below zero for some days.
Load libraries and data
df_tests = pd.read_csv('https://epistat.sciensano.be/Data/COVID19BE_tests.csv', parse_dates=['DATE'])
df_cases = pd.read_csv('https://epistat.sciensano.be/Data/COVID19BE_CASES_AGESEX.csv', parse_dates=['DATE'])
df_cases
| DATE | PROVINCE | REGION | AGEGROUP | SEX | CASES | |
|---|---|---|---|---|---|---|
| 0 | 2020-03-01 | Antwerpen | Flanders | 40-49 | M | 1 |
| 1 | 2020-03-01 | Brussels | Brussels | 10-19 | F | 1 |
| 2 | 2020-03-01 | Brussels | Brussels | 10-19 | M | 1 |
| 3 | 2020-03-01 | Brussels | Brussels | 20-29 | M | 1 |
| 4 | 2020-03-01 | Brussels | Brussels | 30-39 | F | 1 |
| ... | ... | ... | ... | ... | ... | ... |
| 36279 | NaT | VlaamsBrabant | Flanders | 40-49 | M | 3 |
| 36280 | NaT | VlaamsBrabant | Flanders | 50-59 | M | 1 |
| 36281 | NaT | WestVlaanderen | Flanders | 20-29 | F | 1 |
| 36282 | NaT | WestVlaanderen | Flanders | 50-59 | M | 3 |
| 36283 | NaT | NaN | NaN | NaN | NaN | 1 |
36284 rows × 6 columns
Reformat data into Rtlive format
df_cases_per_day = (df_cases
.dropna(subset=['DATE'])
.assign(region='Belgium')
.groupby(['region', 'DATE'], as_index=False)
.agg(cases=('CASES', 'sum'))
.rename(columns={'DATE':'date'})
.set_index(["region", "date"])
)
What's in our basetable:
| cases | ||
|---|---|---|
| region | date | |
| Belgium | 2020-03-01 | 19 |
| 2020-03-02 | 19 | |
| 2020-03-03 | 34 | |
| 2020-03-04 | 53 | |
| 2020-03-05 | 81 | |
| ... | ... | |
| 2020-11-01 | 2660 | |
| 2020-11-02 | 13345 | |
| 2020-11-03 | 11167 | |
| 2020-11-04 | 4019 | |
| 2020-11-05 | 5 |
250 rows × 1 columns
Let's plot the number of cases in function of the time.
ax = df_cases_per_day.loc['Belgium'].plot(figsize=(18,6))
ax.set(ylabel='Number of cases', title='Number of cases for covid-19 and number of positives in Belgium');
We see that the last days are not yet complete. Let's cut off the last two days of reporting.
Calculate the date two days ago:
datetime.date(2020, 11, 3)
# today_minus_two = datetime.date.today() + relativedelta(days=-2)
today_minus_two = datetime.date(2020, 11, 3) # Fix the day
today_minus_two.strftime("%Y-%m-%d")
'2020-11-03'
Replot the cases:
ax = df_cases_per_day.loc['Belgium'][:today_minus_two].plot(figsize=(18,6))
ax.set(ylabel='Number of cases', title='Number of cases for covid-19 and number of positives in Belgium');
Select the Belgium region:
| cases | |
|---|---|
| date | |
| 2020-03-01 | 19 |
| 2020-03-02 | 19 |
| 2020-03-03 | 34 |
| 2020-03-04 | 53 |
| 2020-03-05 | 81 |
| ... | ... |
| 2020-10-30 | 15185 |
| 2020-10-31 | 6243 |
| 2020-11-01 | 2660 |
| 2020-11-02 | 13345 |
| 2020-11-03 | 11167 |
248 rows × 1 columns
Check the types of the columns:
<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 248 entries, 2020-03-01 to 2020-11-03
Data columns (total 1 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 cases 248 non-null int64
dtypes: int64(1)
memory usage: 3.9 KB
Robert Koch Institute method
A basic method to calculate the effective reproduction number is described (among others) in this blogpost. I included the relevant paragraph:
In a recent report (an der Heiden and Hamouda 2020) the RKI described their method for computing R as part of the COVID-19 outbreak as follows (p. 13): For a constant generation time of 4 days, one obtains R as the ratio of new infections in two consecutive time periods each consisting of 4 days. Mathematically, this estimation could be formulated as part of a statistical model:
$$y_{s+4} | y_{s} \sim Po(R \cdot y_{s}), s= 1,2,3,4$$
where $y_{1}, \ldots, y_{4}$ are considered as fixed. From this we obtain
$$\hat{R}{RKI} = \sum$$}^{4} y_{s+4} / \sum_{s=1}^{4} y_{s
Somewhat arbitrary, we denote by $Re(t)$ the above estimate for R when $s=1$ corresponds to time $t-8$, i.e. we assign the obtained value to the last of the 8 values used in the computation.
In Python, we define a lambda function that we apply on a rolling window. Since indexes start from zero, we calculate:
$$\hat{R}{RKI} = \sum$$}^{3} y_{s+4} / \sum_{s=0}^{3} y_{s
| cases | |
|---|---|
| date | |
| 2020-03-01 | NaN |
| 2020-03-02 | NaN |
| 2020-03-03 | NaN |
| 2020-03-04 | NaN |
| 2020-03-05 | NaN |
| ... | ... |
| 2020-10-30 | 1.273703 |
| 2020-10-31 | 0.929291 |
| 2020-11-01 | 0.601838 |
| 2020-11-02 | 0.499806 |
| 2020-11-03 | 0.475685 |
248 rows × 1 columns
The first values are Nan because the window is in the past. If we plot the result, it looks like this:
ax = df.rolling(8).apply(rt).plot(figsize=(16,4), label='Re(t)')
ax.set(ylabel='Re(t)', title='Effective reproduction number estimated with RKI method')
ax.legend(['Re(t)']);
To avoid the spikes due to weekend reporting issue, I first applied a rolling mean on a window of 7 days:
ax = df.rolling(7).mean().rolling(8).apply(rt).plot(figsize=(16,4), label='Re(t)')
ax.set(ylabel='Re(t)', title='Effective reproduction number estimated with RKI method after rolling mean on window of 7 days')
ax.legend(['Re(t)']);
Interactive visualisation in Altair
import altair as alt
alt.Chart(df.rolling(7).mean().rolling(8).apply(rt).fillna(0).reset_index()).mark_line().encode(
x=alt.X('date:T'),
y=alt.Y('cases', title='Re(t)'),
tooltip=['date:T', alt.Tooltip('cases', format='.2f')]
).transform_filter(
alt.datum.date > alt.expr.toDate('2020-03-13')
).properties(
width=600,
title='Effective reproduction number in Belgium based on Robert-Koch Institute method'
)
Making the final visualisation in Altair
In the interactive Altair figure below, we show the $Re(t)$ for the last 14 days. We reduce the rolling mean window to three to see faster reactions.
#collapse
df_plot = df.rolling(7).mean().rolling(8).apply(rt).fillna(0).reset_index()
last_value = str(df_plot.iloc[-1]['cases'].round(2)) + ' ↓'
first_value = str(df_plot[df_plot['date'] == '2020-10-21'].iloc[0]['cases'].round(2)) # + ' ↑'
today_minus_15 = datetime.datetime.today() + relativedelta(days=-15)
today_minus_15_str = today_minus_15.strftime("%Y-%m-%d")
line = alt.Chart(df_plot).mark_line(point=True).encode(
x=alt.X('date:T', axis=alt.Axis(title='Datum', grid=False)),
y=alt.Y('cases', axis=alt.Axis(title='Re(t)', grid=False, labels=False, titlePadding=40)),
tooltip=['date:T', alt.Tooltip('cases', title='Re(t)', format='.2f')]
).transform_filter(
alt.datum.date > alt.expr.toDate(today_minus_15_str)
).properties(
width=600,
height=100
)
hline = alt.Chart(pd.DataFrame({'cases': [1]})).mark_rule().encode(y='cases')
label_right = alt.Chart(df_plot).mark_text(
align='left', dx=5, dy=-10 , size=15
).encode(
x=alt.X('max(date):T', title=None),
text=alt.value(last_value),
)
label_left = alt.Chart(df_plot).mark_text(
align='right', dx=-5, dy=-40, size=15
).encode(
x=alt.X('min(date):T', title=None),
text=alt.value(first_value),
).transform_filter(
alt.datum.date > alt.expr.toDate(today_minus_15_str)
)
source = alt.Chart(
{"values": [{"text": "Data source: Sciensano"}]}
).mark_text(size=12, align='left', dx=-57).encode(
text="text:N"
)
alt.vconcat(line + label_left + label_right + hline, source).configure(
background='#D9E9F0'
).configure_view(
stroke=None, # Remove box around graph
).configure_axisY(
ticks=False,
grid=False,
domain=False
).configure_axisX(
grid=False,
domain=False
).properties(title={
"text": ['Effective reproduction number for the last 14 days in Belgium'],
"subtitle": [f'Estimation based on the number of cases until {today_minus_two.strftime("%Y-%m-%d")} after example of Robert Koch Institute with serial interval of 4'],
}
)
# .configure_axisY(
# labelPadding=50,
# )
To check the calculation, here are the last for values for the number of cases after applying the mean window of 7:
| cases | |
|---|---|
| date | |
| 2020-10-27 | 16067.571429 |
| 2020-10-28 | 16135.857143 |
| 2020-10-29 | 15744.571429 |
| 2020-10-30 | 15218.000000 |
Those must be added together:
cases 63166.0
dtype: float64
And here are the four values, starting four days ago:
| cases | |
|---|---|
| date | |
| 2020-10-31 | 14459.428571 |
| 2020-11-01 | 14140.428571 |
| 2020-11-02 | 13213.428571 |
| 2020-11-03 | 11641.428571 |
These are added together:
cases 53454.714286
dtype: float64
And now we divide those two sums to get the $Re(t)$ of 2020-11-03:
cases 0.846258
dtype: float64
This matches (as expected) the value in the graph. Let's compare with three other sources:
- Alas it does not match the calculation reported by Bart Mesuere on 2020-11-03 based on the RKI model that reports 0.96:
twitter: https://twitter.com/BartMesuere/status/1323519613855059968
-
Also, the more elaborated model from rtliveglobal is not yet that optimistic. Mind that model rtlive start estimating the $Re(t)$ from the number of tests instead of the number of cases. It might be that other reporting delays are involved.
-
epiforecast.io is already below 1 since beginning of November.
Another possiblity is that I made somewhere a mistake. If you spot it, please let me know.
Estimating the effective reproduction number in Belgium
Applying the Bayesian model from Rt.live on Belgium test data.
In this post we estimate the effective reproduction number of COVID-19 in the northern and southern part of Belgium. We apply the Bayesian model of rt.live on Belgian data of COVID-19 tests provided by the goverment.
Install needed packages and software
The current version of pymc3, installed by default in Colab, is version 3.3.7. The requirements for the Bayesian model of rt.live stipulates a more recent version. We first uninstall verions 3.3.7 and then install a version v3.9.3.
Uninstalling pymc3-3.7:
Successfully uninstalled pymc3-3.7
import warnings
warnings.simplefilter(action="ignore", category=FutureWarning)
import pymc3 as pm
import arviz as az
import numpy as np
import pandas as pd
from scipy import stats as sps
import theano
import theano.tensor as tt
from theano.tensor.signal.conv import conv2d
import seaborn as sns
sns.set_context('talk')
from scipy import stats
from matplotlib import pyplot as plt
Running on PyMC3 v3.9.3
Now that we are running a recent version of pymc3, we can install the model:
!pip install git+https://github.com/rtcovidlive/covid-model.git
Unfortunately, this does not work. I pasted the code in this notebook as a workaround.
#hide
# from covid.patients import get_delay_distribution
# p_delay = pd.read_csv('https://raw.githubusercontent.com/rtcovidlive/covid-model/master/data/p_delay.csv')
# From https://github.com/rtcovidlive/covid-model/blob/master/covid/models/generative.py
#collapse
import warnings
warnings.simplefilter(action="ignore", category=FutureWarning)
import pymc3 as pm
import arviz as az
import numpy as np
import pandas as pd
from scipy import stats as sps
import theano
import theano.tensor as tt
from theano.tensor.signal.conv import conv2d
# from covid.patients import get_delay_distribution
class GenerativeModel:
version = "1.0.0"
def __init__(self, region: str, observed: pd.DataFrame, buffer_days=10):
""" Takes a region (ie State) name and observed new positive and
total test counts per day. buffer_days is the default number of
blank days we pad on the leading edge of the time series because
infections occur long before reports and we need to infer values
on those days """
first_index = observed.positive.ne(0).argmax()
observed = observed.iloc[first_index:]
new_index = pd.date_range(
start=observed.index[0] - pd.Timedelta(days=buffer_days),
end=observed.index[-1],
freq="D",
)
observed = observed.reindex(new_index, fill_value=0)
self._trace = None
self._inference_data = None
self.model = None
self.observed = observed
self.region = region
@property
def n_divergences(self):
""" Returns the number of divergences from the current trace """
assert self.trace != None, "Must run sample() first!"
return self.trace["diverging"].nonzero()[0].size
@property
def inference_data(self):
""" Returns an Arviz InferenceData object """
assert self.trace, "Must run sample() first!"
with self.model:
posterior_predictive = pm.sample_posterior_predictive(self.trace)
_inference_data = az.from_pymc3(
trace=self.trace,
posterior_predictive=posterior_predictive,
)
_inference_data.posterior.attrs["model_version"] = self.version
return _inference_data
@property
def trace(self):
""" Returns the trace from a sample() call. """
assert self._trace, "Must run sample() first!"
return self._trace
def _scale_to_positives(self, data):
""" Scales a time series to have the same mean as the observed positives
time series. This is useful because many of the series we infer are
relative to their true values so we make them comparable by putting
them on the same scale. """
scale_factor = self.observed.positive.mean() / np.mean(data)
return scale_factor * data
def _get_generation_time_interval(self):
""" Create a discrete P(Generation Interval)
Source: https://www.ijidonline.com/article/S1201-9712(20)30119-3/pdf """
mean_si = 4.7
std_si = 2.9
mu_si = np.log(mean_si ** 2 / np.sqrt(std_si ** 2 + mean_si ** 2))
sigma_si = np.sqrt(np.log(std_si ** 2 / mean_si ** 2 + 1))
dist = sps.lognorm(scale=np.exp(mu_si), s=sigma_si)
# Discretize the Generation Interval up to 20 days max
g_range = np.arange(0, 20)
gt = pd.Series(dist.cdf(g_range), index=g_range)
gt = gt.diff().fillna(0)
gt /= gt.sum()
gt = gt.values
return gt
def _get_convolution_ready_gt(self, len_observed):
""" Speeds up theano.scan by pre-computing the generation time interval
vector. Thank you to Junpeng Lao for this optimization.
Please see the outbreak simulation math here:
https://staff.math.su.se/hoehle/blog/2020/04/15/effectiveR0.html """
gt = self._get_generation_time_interval()
convolution_ready_gt = np.zeros((len_observed - 1, len_observed))
for t in range(1, len_observed):
begin = np.maximum(0, t - len(gt) + 1)
slice_update = gt[1 : t - begin + 1][::-1]
convolution_ready_gt[
t - 1, begin : begin + len(slice_update)
] = slice_update
convolution_ready_gt = theano.shared(convolution_ready_gt)
return convolution_ready_gt
def build(self):
""" Builds and returns the Generative model. Also sets self.model """
# p_delay = get_delay_distribution()
p_delay = pd.read_csv('https://raw.githubusercontent.com/rtcovidlive/covid-model/master/data/p_delay.csv')
nonzero_days = self.observed.total.gt(0)
len_observed = len(self.observed)
convolution_ready_gt = self._get_convolution_ready_gt(len_observed)
x = np.arange(len_observed)[:, None]
coords = {
"date": self.observed.index.values,
"nonzero_date": self.observed.index.values[self.observed.total.gt(0)],
}
with pm.Model(coords=coords) as self.model:
# Let log_r_t walk randomly with a fixed prior of ~0.035. Think
# of this number as how quickly r_t can react.
log_r_t = pm.GaussianRandomWalk(
"log_r_t",
sigma=0.035,
dims=["date"]
)
r_t = pm.Deterministic("r_t", pm.math.exp(log_r_t), dims=["date"])
# For a given seed population and R_t curve, we calculate the
# implied infection curve by simulating an outbreak. While this may
# look daunting, it's simply a way to recreate the outbreak
# simulation math inside the model:
# https://staff.math.su.se/hoehle/blog/2020/04/15/effectiveR0.html
seed = pm.Exponential("seed", 1 / 0.02)
y0 = tt.zeros(len_observed)
y0 = tt.set_subtensor(y0[0], seed)
outputs, _ = theano.scan(
fn=lambda t, gt, y, r_t: tt.set_subtensor(y[t], tt.sum(r_t * y * gt)),
sequences=[tt.arange(1, len_observed), convolution_ready_gt],
outputs_info=y0,
non_sequences=r_t,
n_steps=len_observed - 1,
)
infections = pm.Deterministic("infections", outputs[-1], dims=["date"])
# Convolve infections to confirmed positive reports based on a known
# p_delay distribution. See patients.py for details on how we calculate
# this distribution.
test_adjusted_positive = pm.Deterministic(
"test_adjusted_positive",
conv2d(
tt.reshape(infections, (1, len_observed)),
tt.reshape(p_delay, (1, len(p_delay))),
border_mode="full",
)[0, :len_observed],
dims=["date"]
)
# Picking an exposure with a prior that exposure never goes below
# 0.1 * max_tests. The 0.1 only affects early values of Rt when
# testing was minimal or when data errors cause underreporting
# of tests.
tests = pm.Data("tests", self.observed.total.values, dims=["date"])
exposure = pm.Deterministic(
"exposure",
pm.math.clip(tests, self.observed.total.max() * 0.1, 1e9),
dims=["date"]
)
# Test-volume adjust reported cases based on an assumed exposure
# Note: this is similar to the exposure parameter in a Poisson
# regression.
positive = pm.Deterministic(
"positive", exposure * test_adjusted_positive,
dims=["date"]
)
# Save data as part of trace so we can access in inference_data
observed_positive = pm.Data("observed_positive", self.observed.positive.values, dims=["date"])
nonzero_observed_positive = pm.Data("nonzero_observed_positive", self.observed.positive[nonzero_days.values].values, dims=["nonzero_date"])
positive_nonzero = pm.NegativeBinomial(
"nonzero_positive",
mu=positive[nonzero_days.values],
alpha=pm.Gamma("alpha", mu=6, sigma=1),
observed=nonzero_observed_positive,
dims=["nonzero_date"]
)
return self.model
def sample(
self,
cores=4,
chains=4,
tune=700,
draws=200,
target_accept=0.95,
init="jitter+adapt_diag",
):
""" Runs the PyMC3 model and stores the trace result in self.trace """
if self.model is None:
self.build()
with self.model:
self._trace = pm.sample(
draws=draws,
cores=cores,
chains=chains,
target_accept=target_accept,
tune=tune,
init=init,
)
return self
Get the data
Read the data from sciensano:
df_tests = pd.read_csv('https://epistat.sciensano.be/Data/COVID19BE_tests.csv', parse_dates=['DATE'])
What is in this dataframe ?
| DATE | PROVINCE | REGION | TESTS_ALL | TESTS_ALL_POS | |
|---|---|---|---|---|---|
| 0 | 2020-03-01 | Antwerpen | Flanders | 18 | 0 |
| 1 | 2020-03-01 | BrabantWallon | Wallonia | 8 | 0 |
| 2 | 2020-03-01 | Brussels | Brussels | 4 | 0 |
| 3 | 2020-03-01 | Hainaut | Wallonia | 5 | 0 |
| 4 | 2020-03-01 | Liège | Wallonia | 8 | 0 |
| ... | ... | ... | ... | ... | ... |
| 2935 | 2020-10-31 | NaN | NaN | 58 | 13 |
| 2936 | 2020-10-31 | Namur | Wallonia | 864 | 387 |
| 2937 | 2020-10-31 | OostVlaanderen | Flanders | 927 | 106 |
| 2938 | 2020-10-31 | VlaamsBrabant | Flanders | 1600 | 259 |
| 2939 | 2020-10-31 | WestVlaanderen | Flanders | 512 | 82 |
2940 rows × 5 columns
We see that we have the number of tests (TESTS_ALL) and the number of positive tests (TEST_ALL_POS) per date, province and region. In this post, we will analyse the three regions: Brussels, Flanders and Wallonia.
Preprocessing
Are the any Nan ?
DATE 0.000000
PROVINCE 0.083333
REGION 0.083333
TESTS_ALL 0.000000
TESTS_ALL_POS 0.000000
dtype: float64
About eight procent of the lines do not have a PROVINCE nor REGION assigned. What should we do with those ? Ignore them ? Let's look how many there are:
ax = df_tests[df_tests['REGION'].isnull()].groupby(['DATE',], dropna=False).sum().plot(figsize=(18, 4))
ax.set(title='Number of covid-19 tests per day not attributed to a region in Belgium', ylabel='Number of tests');
#hide
# (df_tests
# .fillna('Nan')
# .groupby(['DATE','REGION'], as_index=False)['TESTS_ALL']
# .sum().set_index('REGION')['TESTS_ALL']
# # .assign(total=lambda d:d[['Brussels', 'Flanders', 'Wallonia']].sum(axis=1))
# )
REGION
Brussels 4
Flanders 56
Nan 1
Wallonia 21
Brussels 17
...
Wallonia 21127
Brussels 1237
Flanders 3515
Nan 58
Wallonia 2806
Name: TESTS_ALL, Length: 980, dtype: int64
Here we create a function that distributes the non attributed tests according to the number of tests in each region. For example suppose on a day there are 10, 20 and 150 test in Brussels, Flanders and Wallonia respectively. Suppose there are 10 test unattributed in Flanders. Then we add 10 * (10/(10+20+150)) = 10 * (10/180) = 100/180 = 0.55 test to Flanders. The total number of test of Flanders becomes 10.55. We round that to the nearest integer: 11. And we do the same for the other regions Brussels and Wallonia. So we distribute the 10 unattributed tests weighted according to the number of tests in each region.
def redistribute(g, col):
gdata = g.groupby('REGION')[col].sum()
gdata.loc['Brussels'] += gdata.loc['Nan'] * (gdata.loc['Brussels']/(gdata.loc['Brussels'] + gdata.loc['Flanders'] + gdata.loc['Wallonia']))
gdata.loc['Flanders'] += gdata.loc['Nan'] * (gdata.loc['Flanders']/(gdata.loc['Brussels'] + gdata.loc['Flanders'] + gdata.loc['Wallonia']))
gdata.loc['Wallonia'] += gdata.loc['Nan'] * (gdata.loc['Wallonia']/(gdata.loc['Brussels'] + gdata.loc['Flanders'] + gdata.loc['Wallonia']))
gdata.drop(index='Nan', inplace=True)
gdata = np.round(gdata.fillna(0)).astype(int)
return gdata
# Redistribute the nan for the column TESTS_ALL
df_tests_all = (df_tests
.fillna('Nan')
.groupby(['DATE'])
.apply(redistribute, 'TESTS_ALL')
.stack()
.reset_index()
.rename(columns={'DATE':'date', 'REGION':'region', 0:'total'})
)
# Redistribute the nan for the column TESTS_ALL_POS
df_tests_positive = (df_tests
.fillna('Nan')
.groupby(['DATE'])
.apply(redistribute, 'TESTS_ALL_POS')
.stack()
.reset_index()
.rename(columns={'DATE':'date', 'REGION':'region', 0:'positive'})
)
#hide
# (df_tests
# .fillna('Nan')
# .groupby(['DATE','REGION'])['TESTS_ALL']
# .sum().to_frame().unstack()
# # .rename(pandas.index.get_level_values(0), axis='columns')
# .assign(total=lambda d:d.drop(columns=('TESTS_ALL', 'Nan')).sum(axis=1))
# )
# Combine the total number of tests and the number of positive tests into a basetable
df_tests_per_region_day = pd.concat([df_tests_all, df_tests_positive['positive']], axis=1).set_index(['region', 'date'])
# Check if the basetable is ok
assert df_tests_per_region_day.isnull().sum().sum() == 0, 'There are nan in the basetable'
#hide
# Reformat data into Rtlive format
# df_tests_per_region_day = (df_tests
# .groupby(['REGION', 'DATE'], as_index=False)
# .agg(positive=('TESTS_ALL_POS', 'sum'), total=('TESTS_ALL', 'sum'))
# .rename(columns={'REGION':'region', 'DATE':'date'})
# .set_index(["region", "date"])
# )
| total | positive | ||
|---|---|---|---|
| region | date | ||
| Brussels | 2020-03-01 | 4 | 0 |
| Flanders | 2020-03-01 | 57 | 0 |
| Wallonia | 2020-03-01 | 21 | 0 |
| Brussels | 2020-03-02 | 17 | 3 |
| Flanders | 2020-03-02 | 259 | 7 |
| ... | ... | ... | |
| 2020-10-30 | 38154 | 6531 | |
| Wallonia | 2020-10-30 | 21414 | 9011 |
| Brussels | 2020-10-31 | 1246 | 392 |
| Flanders | 2020-10-31 | 3542 | 531 |
| Wallonia | 2020-10-31 | 2827 | 951 |
735 rows × 2 columns
# What regions do we have in the table ?
df_tests_per_region_day.index.get_level_values(0).unique().to_list()
['Brussels', 'Flanders', 'Wallonia']
Re(t) for Flanders
ax = df_tests_per_region_day.loc[region].plot(figsize=(18,6))
ax.set(title=f'Number of tests for covid-19 and number of positives in {region}');
# Remove last two days because tests are not yet fully reported
today_minus_two = datetime.datetime.today() + relativedelta(days=-2)
today_minus_two.strftime("%Y-%m-%d")
'2020-10-30'
ax = df_tests_per_region_day.loc[region][:today_minus_two].plot(figsize=(18,6))
ax.set(title=f'Number of tests for covid-19 and number of positives in {region}');
# Fit the model on the data
df = df_tests_per_region_day.loc[region][:today_minus_two]
gm = GenerativeModel(region, df)
gm.sample()
Only 200 samples in chain.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha, seed, log_r_t]
100.00% [3600/3600 1:10:58<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 700 tune and 200 draw iterations (2_800 + 800 draws total) took 4260 seconds.
<__main__.GenerativeModel at 0x7f382109add8>
#collapse
def summarize_inference_data(inference_data: az.InferenceData):
""" Summarizes an inference_data object into the form that we publish on rt.live """
posterior = inference_data.posterior
hdi_mass = 80
hpdi = az.hdi(posterior.r_t, hdi_prob=hdi_mass / 100).r_t
observed_positive = inference_data.constant_data.observed_positive.to_series()
scale_to_positives = lambda data: observed_positive.mean() / np.mean(data) * data
tests = inference_data.constant_data.tests.to_series()
normalized_positive = observed_positive / tests.clip(0.1 * tests.max())
summary = pd.DataFrame(
data={
"mean": posterior.r_t.mean(["draw", "chain"]),
"median": posterior.r_t.median(["chain", "draw"]),
f"lower_{hdi_mass}": hpdi[:, 0],
f"upper_{hdi_mass}": hpdi[:, 1],
"infections": scale_to_positives(
posterior.infections.mean(["draw", "chain"])
),
"test_adjusted_positive": scale_to_positives(
posterior.test_adjusted_positive.mean(["draw", "chain"])
),
"test_adjusted_positive_raw": scale_to_positives(normalized_positive),
"positive": observed_positive,
"tests": tests,
},
index=pd.Index(posterior.date.values, name="date"),
)
return summary
100.00% [800/800 00:12<00:00]
fig, ax = plt.subplots(figsize=(12, 8))
result.infections.plot(c="C2", label="Expected primary infections")
result.test_adjusted_positive.plot(c="C0", label="Expected positive tests if tests were constant")
result.test_adjusted_positive_raw.plot(c="C1", alpha=.5, label="Expected positive tests", style="--")
gm.observed.positive.plot(c="C7", alpha=.7, label="Reported positive tests")
fig.set_facecolor("w")
ax.legend();
ax.set(title=f"rt.live model inference for {region}", ylabel="number of cases")
sns.despine();
fig, ax = plt.subplots(figsize=(12, 8))
ax.set(title=f"Effective reproduction number for {region}", ylabel="$R_e(t)$")
samples = gm.trace["r_t"]
x = result.index
cmap = plt.get_cmap("Reds")
percs = np.linspace(51, 99, 40)
colors = (percs - np.min(percs)) / (np.max(percs) - np.min(percs))
samples = samples.T
result["median"].plot(c="k", ls='-')
for i, p in enumerate(percs[::-1]):
upper = np.percentile(samples, p, axis=1)
lower = np.percentile(samples, 100-p, axis=1)
color_val = colors[i]
ax.fill_between(x, upper, lower, color=cmap(color_val), alpha=.8)
ax.axhline(1.0, c="k", lw=1, linestyle="--")
sns.despine();
Re(t) for Wallonia
ax = df_tests_per_region_day.loc[region].plot(figsize=(18,6))
ax.set(title=f'Number of tests for covid-19 and number of positives in {region}');
# Remove last two days because tests are not yet fully reported
today_minus_two = datetime.datetime.today() + relativedelta(days=-2)
today_minus_two.strftime("%Y-%m-%d")
'2020-10-30'
ax = df_tests_per_region_day.loc[region][:today_minus_two].plot(figsize=(18,6))
ax.set(title=f'Number of tests for covid-19 and number of positives in {region}');
df = df_tests_per_region_day.loc[region][:today_minus_two]
gm = GenerativeModel(region, df)
gm.sample()
Only 200 samples in chain.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha, seed, log_r_t]
100.00% [3600/3600 1:12:49<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 700 tune and 200 draw iterations (2_800 + 800 draws total) took 4371 seconds.
<__main__.GenerativeModel at 0x7f380ac35c88>
100.00% [800/800 00:12<00:00]
fig, ax = plt.subplots(figsize=(12, 8))
result.infections.plot(c="C2", label="Expected primary infections")
result.test_adjusted_positive.plot(c="C0", label="Expected positive tests if tests were constant")
result.test_adjusted_positive_raw.plot(c="C1", alpha=.5, label="Expected positive tests", style="--")
gm.observed.positive.plot(c="C7", alpha=.7, label="Reported positive tests")
fig.set_facecolor("w")
ax.legend();
ax.set(title=f"rt.live model inference for {region}", ylabel="number of cases")
sns.despine();
fig, ax = plt.subplots(figsize=(12, 8))
ax.set(title=f"Effective reproduction number for {region}", ylabel="$R_e(t)$")
samples = gm.trace["r_t"]
x = result.index
cmap = plt.get_cmap("Reds")
percs = np.linspace(51, 99, 40)
colors = (percs - np.min(percs)) / (np.max(percs) - np.min(percs))
samples = samples.T
result["median"].plot(c="k", ls='-')
for i, p in enumerate(percs[::-1]):
upper = np.percentile(samples, p, axis=1)
lower = np.percentile(samples, 100-p, axis=1)
color_val = colors[i]
ax.fill_between(x, upper, lower, color=cmap(color_val), alpha=.8)
ax.axhline(1.0, c="k", lw=1, linestyle="--")
sns.despine();
My talk at data science leuven
Links to video and slides of the talk and thanking people.
Talk material
On 23 April 2020, I was invited for a talk at Data science Leuven. I talked about how you can explore and explain the results of a clustering exercise. The target audience are data scientists that that have notions of how to cluster data and that want to improve their skills.
The video is recorded on Youtube:
youtube: https://youtu.be/hk0arqhcX9U?t=3570
You can see the slides here: slides
The talk itself is based on this notebook that I published on this blog yesterday and that I used to demo during the talk.
The host of the conference was Istvan Hajnal. He tweeted the following:
twitter: https://twitter.com/dsleuven/status/1253391470444371968
He also took the R out of my family name NachteRgaele. Troubles with R, it's becoming a story of my life... 
Behind the scene Kris Peeters calmly took the heat of doing the live streaming. 
Almost Pydata quality! Big thanks to the whole Data Science Leuven team that is doing all this on voluntary basis.
Standing on the shoulders of the giants
This talks was not possible without the awesome Altair visualisation library made by Jake VanderPlas. Secondly, it builds upon the open source Shap library made by Scott Lundberg. Those two libraries had a major impact on my daily work as datascientist at Colruyt group. They inspired me in trying to give back to the open source community with this talk. 
If you want to learn how to use Altair I recommend the tutorial made by Vincent Warmerdam on his calm code site: https://calmcode.io/altair/introduction.htm
I would also like to thank my collegues at work who endured the dry-run of this talk and who made the suggestion to try to use a classifier to explain the clustering result. Top team!
Awesome fastpages
Finally, this blog is build with the awesome fastpages. I can now share a rendered Jupyter notebook, with working interactive demos, that can be opened in My binder or Google Colab with one click on a button. This means that readers can directly tinker around with the code and methods discussed in the talk. All you need is a browser and an internet connection. So thank you Jeremy Howard, Hamel Husain, and the fastdotai team for pulling this off. Thank you Hamel Husain for your Github Actions. I will cast for two how awesome this all is.
Explain clusters to business with Altair and Shapley values
Everyone that calls herselve a data scientist has at least clustered the Iris dataset. This notebook goes beyond the classical dimension reduction and clustering. I gives you two extra superpowerS to explain the resulting clusters to your client. - First: I'll show how we can add extra insight by using interactive charts made with interactive graphs in Altair. - Second I explain and show how to derive important clues from Shap values by training a classification model on the clustering result. With the Altair and shap libraries in your datascience toolbelt, you will excel at the clustering tasks thrown at you.
- image: pca_cluster_altair_view.png
The data is a set of about 5000 wines from the UCI Machine learning Repository. The dataset is related to the white variants of the Portuguese "Vinho Verde" wine. There are 11 features that describe chemical characteristics of the wines. The task is to find clusters of wine that are in a way similar to each other. By reducing the 5000 wines to a small number of groups of wine, you can give strategic advise to your business by generalising per cluster instead of per wine.
We are not using the quality of the wine. This notebook is to illustrate a unsupervised clustering approach. We start from the classic PCA dimension reduction for visualisation and Kmeans for clustering. Other dimension reduction techniques (LDA, UMAP, t-sne, ivis, ...) and clustering techniques (density based, aglomerative, gaussian mixture, ...) are left as an excercise for the reader.
References
Dua, D. and Karra Taniskidou, E. (2017). UCI Machine Learning Repository [http://archive.ics.uci.edu/ml]. Irvine, CA: University of California, School of Information and Computer Science.
# Load python libraries for data handling and plotting
import numpy as np
import pandas as pd
import altair as alt
import matplotlib.pyplot as plt
# Load the data set with wines from the internet
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-white.csv', sep=';')
| fixed acidity | volatile acidity | citric acid | residual sugar | chlorides | free sulfur dioxide | total sulfur dioxide | density | pH | sulphates | alcohol | quality | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7.0 | 0.27 | 0.36 | 20.7 | 0.045 | 45.0 | 170.0 | 1.0010 | 3.00 | 0.45 | 8.8 | 6 |
| 1 | 6.3 | 0.30 | 0.34 | 1.6 | 0.049 | 14.0 | 132.0 | 0.9940 | 3.30 | 0.49 | 9.5 | 6 |
| 2 | 8.1 | 0.28 | 0.40 | 6.9 | 0.050 | 30.0 | 97.0 | 0.9951 | 3.26 | 0.44 | 10.1 | 6 |
| 3 | 7.2 | 0.23 | 0.32 | 8.5 | 0.058 | 47.0 | 186.0 | 0.9956 | 3.19 | 0.40 | 9.9 | 6 |
| 4 | 7.2 | 0.23 | 0.32 | 8.5 | 0.058 | 47.0 | 186.0 | 0.9956 | 3.19 | 0.40 | 9.9 | 6 |
(4898, 12)
Index(['fixed acidity', 'volatile acidity', 'citric acid', 'residual sugar',
'chlorides', 'free sulfur dioxide', 'total sulfur dioxide', 'density',
'pH', 'sulphates', 'alcohol', 'quality'],
dtype='object')
# Define the standard X (feature matrix) and target series y (not used in here)
X = df.drop(columns='quality')
all_features = X.columns
y = df['quality']
| fixed acidity | volatile acidity | citric acid | residual sugar | chlorides | free sulfur dioxide | total sulfur dioxide | density | pH | sulphates | alcohol | quality | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 |
| mean | 6.854788 | 0.278241 | 0.334192 | 6.391415 | 0.045772 | 35.308085 | 138.360657 | 0.994027 | 3.188267 | 0.489847 | 10.514267 | 5.877909 |
| std | 0.843868 | 0.100795 | 0.121020 | 5.072058 | 0.021848 | 17.007137 | 42.498065 | 0.002991 | 0.151001 | 0.114126 | 1.230621 | 0.885639 |
| min | 3.800000 | 0.080000 | 0.000000 | 0.600000 | 0.009000 | 2.000000 | 9.000000 | 0.987110 | 2.720000 | 0.220000 | 8.000000 | 3.000000 |
| 25% | 6.300000 | 0.210000 | 0.270000 | 1.700000 | 0.036000 | 23.000000 | 108.000000 | 0.991723 | 3.090000 | 0.410000 | 9.500000 | 5.000000 |
| 50% | 6.800000 | 0.260000 | 0.320000 | 5.200000 | 0.043000 | 34.000000 | 134.000000 | 0.993740 | 3.180000 | 0.470000 | 10.400000 | 6.000000 |
| 75% | 7.300000 | 0.320000 | 0.390000 | 9.900000 | 0.050000 | 46.000000 | 167.000000 | 0.996100 | 3.280000 | 0.550000 | 11.400000 | 6.000000 |
| max | 14.200000 | 1.100000 | 1.660000 | 65.800000 | 0.346000 | 289.000000 | 440.000000 | 1.038980 | 3.820000 | 1.080000 | 14.200000 | 9.000000 |
# Add interactivity
alt.Chart(df).mark_point().encode(x='fixed acidity', y='volatile acidity', color='quality:N', tooltip=['alcohol', 'quality']).interactive()
Scaling
From the describe, we see that domains of the feature differ widely. Feature 'fixed acidity' has mean 6.854788, while feature 'volatile acidity' has mean 0.278241. This is a sign that are on a different scale. We scale the features first so that we can use them together.
# When features have different scale we have to scale them so that we can use them together
from sklearn.preprocessing import RobustScaler
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
# scaler = RobustScaler() # Take the robust scaler when data contains outliers that you want to remove
PCA
Perform principal component analysis to get an idea of the dimensionality of the wine dataset. Next reduce to two dimension so that we can make a 2D scatter plot were each dot is a wine from the set.
df_plot = pd.DataFrame({'Component Number': 1+np.arange(X.shape[1]),
'Cumulative explained variance': np.cumsum(pca.explained_variance_ratio_)})
alt.Chart(df_plot).mark_bar().encode(
x=alt.X('Component Number:N', axis=alt.Axis(labelAngle=0)),
y=alt.Y('Cumulative explained variance', axis=alt.Axis(format='%', title='Percentage')),
tooltip=[alt.Tooltip('Cumulative explained variance', format='.0%')]
).properties(
title='Cumulative explained variance'
).properties(
width=400
)
We see that almost all features are needed to explain all the variance. Only with 9 comoponent we can explain 97% of the variance. This means that we should use all features from the dataset and feature selection is not necessary in this case.
PCA with 2 Dimensions
Perform dimension reduction to two dimentions with PCA to be able to draw all the wines in one graph (not for the clustering!)
# Add first to PCA components to the dataset so we can plot it
df['pca1'] = X_pca[:,0]
df['pca2'] = X_pca[:,1]
0 0.448755
1 0.448755
2 0.448755
3 0.448755
4 0.448755
...
4893 0.448755
4894 0.297468
4895 0.448755
4896 0.179665
4897 0.448755
Name: member, Length: 4898, dtype: float64
selection = alt.selection_multi(fields=['quality'], bind='legend')
df['quality_weight'] = df['quality'].map(df['quality'].value_counts(normalize=True).to_dict())
# Draw 20% stratified sample
alt.Chart(df.sample(1000, weights='quality_weight')).mark_circle(size=60).encode(
x=alt.X('pca1', title='First component'),
y=alt.Y('pca2', title='Second component'),
color=alt.Color('quality:N'),
tooltip=['quality'],
opacity=alt.condition(selection, alt.value(1), alt.value(0.2))
).properties(
title='PCA analyse',
width=600,
height=400
).add_selection(
selection
)
pca1 = alt.Chart(df_twod_pca.reset_index()).mark_bar().encode(
y=alt.Y('index:O', title=None),
x='pca1',
color=alt.Color('pca1', scale=alt.Scale(scheme='viridis')),
tooltip = [alt.Tooltip('index', title='Feature'), alt.Tooltip('pca1', format='.2f')]
)
pca2 = alt.Chart(df_twod_pca.reset_index()).mark_bar().encode(
y=alt.Y('index:O', title=None),
x='pca2',
color=alt.Color('pca2', scale=alt.Scale(scheme='viridis')),
tooltip = [alt.Tooltip('index', title='Feature'), alt.Tooltip('pca2', format='.2f')]
)
(pca1 & pca2).properties(
title='Loadings of the first two principal components'
)
Kmeans clustering
Determine the number of cluster for Kmeans clustering by lopping from 2 to 11 cluster. Calculate for each result the within-cluster variation (inertia), the silhoutte and the Davies-Bouldin index. Use the elbow method to determine the number of clusters. The elbow method seeks the value of k after which the clustering quality improves only marginally.
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score, davies_bouldin_score
km_scores= []
km_silhouette = []
km_db_score = []
for i in range(2,X.shape[1]):
km = KMeans(n_clusters=i, random_state=1301).fit(X_scaled)
preds = km.predict(X_scaled)
print(f'Score for number of cluster(s) {i}: {km.score(X_scaled):.3f}')
km_scores.append(-km.score(X_scaled))
silhouette = silhouette_score(X_scaled,preds)
km_silhouette.append(silhouette)
print(f'Silhouette score for number of cluster(s) {i}: {silhouette:.3f}')
db = davies_bouldin_score(X_scaled,preds)
km_db_score.append(db)
print(f'Davies Bouldin score for number of cluster(s) {i}: {db:.3f}')
print('-'*100)
Score for number of cluster(s) 2: -42548.672
Silhouette score for number of cluster(s) 2: 0.214
Davies Bouldin score for number of cluster(s) 2: 1.775
----------------------------------------------------------------------------------------------------
Score for number of cluster(s) 3: -39063.495
Silhouette score for number of cluster(s) 3: 0.144
Davies Bouldin score for number of cluster(s) 3: 2.097
----------------------------------------------------------------------------------------------------
Score for number of cluster(s) 4: -35986.918
Silhouette score for number of cluster(s) 4: 0.159
Davies Bouldin score for number of cluster(s) 4: 1.809
----------------------------------------------------------------------------------------------------
Score for number of cluster(s) 5: -33699.043
Silhouette score for number of cluster(s) 5: 0.144
Davies Bouldin score for number of cluster(s) 5: 1.768
----------------------------------------------------------------------------------------------------
Score for number of cluster(s) 6: -31973.251
Silhouette score for number of cluster(s) 6: 0.146
Davies Bouldin score for number of cluster(s) 6: 1.693
----------------------------------------------------------------------------------------------------
Score for number of cluster(s) 7: -30552.998
Silhouette score for number of cluster(s) 7: 0.126
Davies Bouldin score for number of cluster(s) 7: 1.847
----------------------------------------------------------------------------------------------------
Score for number of cluster(s) 8: -29361.568
Silhouette score for number of cluster(s) 8: 0.128
Davies Bouldin score for number of cluster(s) 8: 1.790
----------------------------------------------------------------------------------------------------
Score for number of cluster(s) 9: -28198.302
Silhouette score for number of cluster(s) 9: 0.128
Davies Bouldin score for number of cluster(s) 9: 1.760
----------------------------------------------------------------------------------------------------
Score for number of cluster(s) 10: -27444.897
Silhouette score for number of cluster(s) 10: 0.118
Davies Bouldin score for number of cluster(s) 10: 1.843
----------------------------------------------------------------------------------------------------
df_plot = pd.DataFrame({'Number of clusters':[i for i in range(2,X.shape[1])],'kmean score': km_scores})
alt.Chart(df_plot).mark_line(point=True).encode(
x=alt.X('Number of clusters:N', axis=alt.Axis(labelAngle=0)),
y=alt.Y('kmean score'),
tooltip=[alt.Tooltip('kmean score', format='.2f')]
).properties(
title='Kmean score ifo number of cluster'
).properties(
title='The elbow method for determining number of clusters',
width=400
)
df_plot = pd.DataFrame({'Number of clusters':[i for i in range(2,X.shape[1])],'silhouette score': km_silhouette})
alt.Chart(df_plot).mark_line(point=True).encode(
x=alt.X('Number of clusters:N', axis=alt.Axis(labelAngle=0)),
y=alt.Y('silhouette score'),
tooltip=[alt.Tooltip('silhouette score', format='.2f')]
).properties(
title='Silhouette score ifo number of cluster',
width=400
)
df_plot = pd.DataFrame({'Number of clusters':[i for i in range(2, X.shape[1])],'davies bouldin score': km_db_score})
alt.Chart(df_plot).mark_line(point=True).encode(
x=alt.X('Number of clusters:N', axis=alt.Axis(labelAngle=0)),
y=alt.Y('davies bouldin score'),
tooltip=[alt.Tooltip('davies bouldin score', format='.2f')]
).properties(
title='Davies Bouldin score ifo number of cluster',
width=400
)
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.cm as cm
X = X.values
range_n_clusters = [2, 3, 4, 5, 6]
for n_clusters in range_n_clusters:
# Create a subplot with 1 row and 2 columns
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(18, 7)
# The 1st subplot is the silhouette plot
# The silhouette coefficient can range from -1, 1 but in this example all
# lie within [-0.1, 1]
ax1.set_xlim([-0.1, 1])
# The (n_clusters+1)*10 is for inserting blank space between silhouette
# plots of individual clusters, to demarcate them clearly.
ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])
# Initialize the clusterer with n_clusters value and a random generator
# seed of 10 for reproducibility.
clusterer = KMeans(n_clusters=n_clusters, random_state=10)
cluster_labels = clusterer.fit_predict(X)
# The silhouette_score gives the average value for all the samples.
# This gives a perspective into the density and separation of the formed
# clusters
silhouette_avg = silhouette_score(X, cluster_labels)
print("For n_clusters =", n_clusters,
"The average silhouette_score is :", silhouette_avg)
# Compute the silhouette scores for each sample
sample_silhouette_values = silhouette_samples(X, cluster_labels)
y_lower = 10
for i in range(n_clusters):
# Aggregate the silhouette scores for samples belonging to
# cluster i, and sort them
ith_cluster_silhouette_values = \
sample_silhouette_values[cluster_labels == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i) / n_clusters)
ax1.fill_betweenx(np.arange(y_lower, y_upper),
0, ith_cluster_silhouette_values,
facecolor=color, edgecolor=color, alpha=0.7)
# Label the silhouette plots with their cluster numbers at the middle
ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
# Compute the new y_lower for next plot
y_lower = y_upper + 10 # 10 for the 0 samples
ax1.set_title("The silhouette plot for the various clusters.")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
# The vertical line for average silhouette score of all the values
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
ax1.set_yticks([]) # Clear the yaxis labels / ticks
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
# 2nd Plot showing the actual clusters formed
colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
ax2.scatter(X[:, 0], X[:, 1], marker='.', s=30, lw=0, alpha=0.7,
c=colors, edgecolor='k')
# Labeling the clusters
centers = clusterer.cluster_centers_
# Draw white circles at cluster centers
ax2.scatter(centers[:, 0], centers[:, 1], marker='o',
c="white", alpha=1, s=200, edgecolor='k')
for i, c in enumerate(centers):
ax2.scatter(c[0], c[1], marker='$%d$' % i, alpha=1,
s=50, edgecolor='k')
ax2.set_title("The visualization of the clustered data.")
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")
plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
"with n_clusters = %d" % n_clusters),
fontsize=14, fontweight='bold')
plt.show()
For n_clusters = 2 The average silhouette_score is : 0.5062782327345698
For n_clusters = 3 The average silhouette_score is : 0.4125412743885912
For n_clusters = 4 The average silhouette_score is : 0.3748324919186734
For n_clusters = 5 The average silhouette_score is : 0.3437053439455249
For n_clusters = 6 The average silhouette_score is : 0.313821767576001
Make three clusters
Since we have a high Davies Boldin and low Silhoutte score for k=3 we select to cluster into three clusters. Another option could be to use the Gaussian Likelihood score. In this notebook another analysis reported also 3 clusters.
km = KMeans(n_clusters=3, random_state=1301).fit(X_scaled)
preds = km.predict(X_scaled)
pd.Series(preds).value_counts() # How many wines are in each cluster ?
0 1801
1 1629
2 1468
dtype: int64
# Add the scaled data with the input features
for i,c in enumerate(all_features):
df_km[c] = X_scaled[:,i]
domain = [0, 1, 2]
range_ = ['red', 'darkblue', 'green']
selection = alt.selection_multi(fields=['cluster'], bind='legend')
pca = alt.Chart(df_km).mark_circle(size=20).encode(
x='pca1',
y='pca2',
color=alt.Color('cluster:N', scale=alt.Scale(domain=domain, range=range_)),
opacity=alt.condition(selection, alt.value(1), alt.value(0.1)),
tooltip = list(all_features)
).add_selection(
selection
)
pca
Now we will plot the all the wines on a two dimensional plane. On the right, you get boxplots for every feature. The cool thing is now that with the mouse you can select by drawing a brush over the points (click, hold button and drag the mouse) and get immediate updates boxplots of the features of the selected wines. A such you can interactively gain some insight in what the cluster might mean.
brush = alt.selection(type='interval')
domain = [0, 1, 2]
range_ = ['red', 'darkblue', 'green']
points = alt.Chart(df_km).mark_circle(size=60).encode(
x='pca1',
y='pca2',
color = alt.condition(brush, 'cluster:N', alt.value('lightgray')),
tooltip = list(all_features)
).add_selection(brush)
boxplots = alt.vconcat()
for measure in all_features:
boxplot = alt.Chart(df_km).mark_boxplot().encode(
x =alt.X(measure, axis=alt.Axis(titleX=470, titleY=0)),
).transform_filter(
brush
)
boxplots &= boxplot
chart = alt.hconcat(points, boxplots)
# chart.save('cluster_pca_n_3.html'))
chart
AS you can't select al wine from one cluster with the rectangular brush, we make a plot for each cluster and boxplots of the features values of that cluster.
def plot_cluster(df, selected_columns, clusternr):
points = alt.Chart(df).mark_circle(size=60).encode(
x=alt.X('pca1', title='Principal component 1 (pca1)'),
y=alt.Y('pca2', title='Principal component 2 (pca1)'),
color = alt.condition(alt.FieldEqualPredicate(field='cluster', equal=clusternr), 'cluster:N', alt.value('lightgray')),
tooltip = list(all_features)+['cluster'],
)
boxplots = alt.vconcat()
for measure in [c for c in selected_columns]:
boxplot = alt.Chart(df).mark_boxplot().encode(
x =alt.X(measure, axis=alt.Axis(titleX=480, titleY=0)),
).transform_filter(
alt.FieldEqualPredicate(field='cluster', equal=clusternr)
)
boxplots &= boxplot
return points, boxplots
points, boxplots = plot_cluster(df_km, all_features, 0)
c0 = alt.hconcat(points, boxplots).properties(title='Cluster 0')
points, boxplots = plot_cluster(df_km, all_features, 1)
c1 = alt.hconcat(points, boxplots).properties(title='Cluster 1')
points, boxplots = plot_cluster(df_km, all_features, 2)
c2 = alt.hconcat(points, boxplots).properties(title='Cluster 2')
I might still be difficult to explain the clusters. We will now build a multiclass classifier to predict the cluster from the features. Next we will use the Shapley values to explain the clusters.
Light gbm classifier
{'boosting_type': 'gbdt',
'class_weight': None,
'colsample_bytree': 1.0,
'importance_type': 'split',
'learning_rate': 0.1,
'max_depth': -1,
'min_child_samples': 20,
'min_child_weight': 0.001,
'min_split_gain': 0.0,
'n_estimators': 100,
'n_jobs': -1,
'num_leaves': 31,
'objective': None,
'random_state': None,
'reg_alpha': 0.0,
'reg_lambda': 0.0,
'silent': True,
'subsample': 1.0,
'subsample_for_bin': 200000,
'subsample_freq': 0}
params['objective'] = 'multiclass' # the target to predict is the number of the cluster
params['is_unbalance'] = True
params['n_jobs'] = -1
params['random_state'] = 1301
LGBMClassifier(boosting_type='gbdt', class_weight=None, colsample_bytree=1.0,
importance_type='split', is_unbalance=True, learning_rate=0.1,
max_depth=-1, min_child_samples=20, min_child_weight=0.001,
min_split_gain=0.0, n_estimators=100, n_jobs=-1, num_leaves=31,
objective='multiclass', random_state=1301, reg_alpha=0.0,
reg_lambda=0.0, silent=True, subsample=1.0,
subsample_for_bin=200000, subsample_freq=0)
Requirement already satisfied: shap in /usr/local/lib/python3.6/dist-packages (0.35.0)
Requirement already satisfied: pandas in /usr/local/lib/python3.6/dist-packages (from shap) (1.0.3)
Requirement already satisfied: scikit-learn in /usr/local/lib/python3.6/dist-packages (from shap) (0.22.2.post1)
Requirement already satisfied: scipy in /usr/local/lib/python3.6/dist-packages (from shap) (1.4.1)
Requirement already satisfied: numpy in /usr/local/lib/python3.6/dist-packages (from shap) (1.18.2)
Requirement already satisfied: tqdm>4.25.0 in /usr/local/lib/python3.6/dist-packages (from shap) (4.38.0)
Requirement already satisfied: pytz>=2017.2 in /usr/local/lib/python3.6/dist-packages (from pandas->shap) (2018.9)
Requirement already satisfied: python-dateutil>=2.6.1 in /usr/local/lib/python3.6/dist-packages (from pandas->shap) (2.8.1)
Requirement already satisfied: joblib>=0.11 in /usr/local/lib/python3.6/dist-packages (from scikit-learn->shap) (0.14.1)
Requirement already satisfied: six>=1.5 in /usr/local/lib/python3.6/dist-packages (from python-dateutil>=2.6.1->pandas->shap) (1.12.0)
Setting feature_perturbation = "tree_path_dependent" because no background data was given.
From the Shapley values we see that the feature density has the highest impact on the model to predict the clusters. Let's have a look the Shapley values per cluster. The acidity features pH and fixed acidity has only impact on cluster 1 and 2 but almost none on cluster 0.
Shapley values for the three clusters
for cnr in df_km['cluster'].unique():
shap.summary_plot(shap_values[cnr], X, max_display=30, show=False)
plt.title(f'Cluster {cnr}')
plt.show()
To explain the clusters, we will plot the three clusters and the boxplot of the features ordered with the feature importance.
Explain cluster 0
cnr = 0
feature_order = np.argsort(np.sum(np.abs(shap_values[cnr]), axis=0))
points, boxplots = plot_cluster(df_km, [X.columns[i] for i in feature_order][::-1][:6], 0)
c0 = alt.hconcat(points, boxplots).properties(title='Cluster 0')
c0
cnr = 0
shap.summary_plot(shap_values[cnr], X, max_display=30, show=False)
plt.title(f'Cluster {cnr}')
plt.show()
Cluster 0 can be describe as wines with: - high density - high total sulfur dioxide - high free sulfur dioxide
Explain cluster 1
Index(['fixed acidity', 'volatile acidity', 'citric acid', 'residual sugar',
'chlorides', 'free sulfur dioxide', 'total sulfur dioxide', 'density',
'pH', 'sulphates', 'alcohol', 'quality_weight'],
dtype='object')
cnr = 1
feature_order = np.argsort(np.sum(np.abs(shap_values[cnr]), axis=0))
points, boxplots = plot_cluster(df_km, [X.columns[i] for i in feature_order][::-1][:6], cnr)
c1 = alt.hconcat(points, boxplots).properties(title=f'Cluster {cnr}')
c1
cnr = 1
shap.summary_plot(shap_values[cnr], X, max_display=30, show=False)
plt.title(f'Cluster {cnr}')
plt.show()
Cluster 1 contains wines with: - high pH - low fixed acidity - low density (opposite of cluster 0) - low citric acid - high on sulphates
Explain cluster 2
cnr = 2
feature_order = np.argsort(np.sum(np.abs(shap_values[cnr]), axis=0))
points, boxplots = plot_cluster(df_km, [X.columns[i] for i in feature_order][::-1][:6], cnr)
c2 = alt.hconcat(points, boxplots).properties(title=f'Cluster {cnr}')
c2
cnr = 2
shap.summary_plot(shap_values[cnr], X, max_display=30, show=False)
plt.title(f'Cluster {cnr}')
plt.show()
Cluster 2 contains wines with: - high fixed acidity - low pH (opposite of cluster 1) - low density (opposite of cluster 0)
How is the quality of the whines in each cluster ?
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| cluster | ||||||||
| 0 | 1801.0 | 5.606330 | 0.750514 | 3.0 | 5.0 | 6.0 | 6.0 | 8.0 |
| 1 | 1629.0 | 6.150399 | 0.905265 | 3.0 | 6.0 | 6.0 | 7.0 | 9.0 |
| 2 | 1468.0 | 5.908719 | 0.918554 | 3.0 | 5.0 | 6.0 | 6.0 | 9.0 |
# Let's plot the distributions of quality score per cluster
alt.Chart(df_km).transform_density(
density='quality',
bandwidth=0.3,
groupby=['cluster'],
extent= [3, 9],
counts = True,
steps=200
).mark_area().encode(
alt.X('value:Q'),
alt.Y('density:Q', stack='zero'),
alt.Color('cluster:N')
).properties(
title='Distribution of quality of the wines per cluster',
width=400,
height=100
)
We see that the quality has a similar distribution in each cluster.
Regional covid-19 mortality in Belgium per gender and age
Combines the mortality number of the last 10 year with those of covid-19 this year.
df_inhab = pd.read_excel('https://statbel.fgov.be/sites/default/files/files/opendata/bevolking%20naar%20woonplaats%2C%20nationaliteit%20burgelijke%20staat%20%2C%20leeftijd%20en%20geslacht/TF_SOC_POP_STRUCT_2019.xlsx')
| CD_REFNIS | TX_DESCR_NL | TX_DESCR_FR | CD_DSTR_REFNIS | TX_ADM_DSTR_DESCR_NL | TX_ADM_DSTR_DESCR_FR | CD_PROV_REFNIS | TX_PROV_DESCR_NL | TX_PROV_DESCR_FR | CD_RGN_REFNIS | TX_RGN_DESCR_NL | TX_RGN_DESCR_FR | CD_SEX | CD_NATLTY | TX_NATLTY_NL | TX_NATLTY_FR | CD_CIV_STS | TX_CIV_STS_NL | TX_CIV_STS_FR | CD_AGE | MS_POPULATION | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 11001 | Aartselaar | Aartselaar | 11000 | Arrondissement Antwerpen | Arrondissement d’Anvers | 10000.0 | Provincie Antwerpen | Province d’Anvers | 2000 | Vlaams Gewest | Région flamande | F | BEL | Belgen | Belges | 4 | Gescheiden | Divorcé | 69 | 11 |
| 1 | 11001 | Aartselaar | Aartselaar | 11000 | Arrondissement Antwerpen | Arrondissement d’Anvers | 10000.0 | Provincie Antwerpen | Province d’Anvers | 2000 | Vlaams Gewest | Région flamande | F | BEL | Belgen | Belges | 4 | Gescheiden | Divorcé | 80 | 3 |
| 2 | 11001 | Aartselaar | Aartselaar | 11000 | Arrondissement Antwerpen | Arrondissement d’Anvers | 10000.0 | Provincie Antwerpen | Province d’Anvers | 2000 | Vlaams Gewest | Région flamande | M | BEL | Belgen | Belges | 4 | Gescheiden | Divorcé | 30 | 2 |
| 3 | 11001 | Aartselaar | Aartselaar | 11000 | Arrondissement Antwerpen | Arrondissement d’Anvers | 10000.0 | Provincie Antwerpen | Province d’Anvers | 2000 | Vlaams Gewest | Région flamande | F | BEL | Belgen | Belges | 4 | Gescheiden | Divorcé | 48 | 26 |
| 4 | 11001 | Aartselaar | Aartselaar | 11000 | Arrondissement Antwerpen | Arrondissement d’Anvers | 10000.0 | Provincie Antwerpen | Province d’Anvers | 2000 | Vlaams Gewest | Région flamande | F | BEL | Belgen | Belges | 4 | Gescheiden | Divorcé | 76 | 2 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 463376 | 93090 | Viroinval | Viroinval | 93000 | Arrondissement Philippeville | Arrondissement de Philippeville | 90000.0 | Provincie Namen | Province de Namur | 3000 | Waals Gewest | Région wallonne | F | BEL | Belgen | Belges | 3 | Weduwstaat | Veuf | 73 | 10 |
| 463377 | 93090 | Viroinval | Viroinval | 93000 | Arrondissement Philippeville | Arrondissement de Philippeville | 90000.0 | Provincie Namen | Province de Namur | 3000 | Waals Gewest | Région wallonne | M | BEL | Belgen | Belges | 3 | Weduwstaat | Veuf | 64 | 1 |
| 463378 | 93090 | Viroinval | Viroinval | 93000 | Arrondissement Philippeville | Arrondissement de Philippeville | 90000.0 | Provincie Namen | Province de Namur | 3000 | Waals Gewest | Région wallonne | M | BEL | Belgen | Belges | 3 | Weduwstaat | Veuf | 86 | 3 |
| 463379 | 93090 | Viroinval | Viroinval | 93000 | Arrondissement Philippeville | Arrondissement de Philippeville | 90000.0 | Provincie Namen | Province de Namur | 3000 | Waals Gewest | Région wallonne | M | ETR | niet-Belgen | non-Belges | 3 | Weduwstaat | Veuf | 74 | 1 |
| 463380 | 93090 | Viroinval | Viroinval | 93000 | Arrondissement Philippeville | Arrondissement de Philippeville | 90000.0 | Provincie Namen | Province de Namur | 3000 | Waals Gewest | Région wallonne | M | BEL | Belgen | Belges | 3 | Weduwstaat | Veuf | 52 | 1 |
463381 rows × 21 columns
array(['Provincie Antwerpen', 'Provincie Vlaams-Brabant',
'Provincie Waals-Brabant', 'Provincie West-Vlaanderen',
'Provincie Oost-Vlaanderen', 'Provincie Henegouwen',
'Provincie Luik', 'Provincie Limburg', 'Provincie Luxemburg',
'Provincie Namen'], dtype=object)
array(['Brussels', 'Liège', 'Limburg', 'OostVlaanderen', 'VlaamsBrabant',
'Antwerpen', 'WestVlaanderen', 'BrabantWallon', 'Hainaut', 'Namur',
nan, 'Luxembourg'], dtype=object)
['Antwerpen',
'Vlaams-Brabant',
'Waals-Brabant',
'West-Vlaanderen',
'Oost-Vlaanderen',
'Henegouwen',
'Luik',
'Limburg',
'Luxemburg',
'Namen']
map_statbel_provence_to_sc_provence = {'Provincie Antwerpen':'Antwerpen', 'Provincie Vlaams-Brabant':'VlaamsBrabant',
'Provincie Waals-Brabant':'BrabantWallon', 'Provincie West-Vlaanderen':'WestVlaanderen',
'Provincie Oost-Vlaanderen':'OostVlaanderen', 'Provincie Henegouwen':'Hainaut',
'Provincie Luik':'Liège', 'Provincie Limburg':'Limburg', 'Provincie Luxemburg':'Luxembourg',
'Provincie Namen':'Namur'}
array(['10-19', '20-29', '30-39', '40-49', '50-59', '70-79', '60-69',
'0-9', '90+', '80-89', nan], dtype=object)
df_inhab['AGEGROUP'] =pd.cut(df_inhab['CD_AGE'], bins=[0,10,20,30,40,50,60,70,80,90,200], labels=['0-9','10-19','20-29','30-39','40-49','50-59','60-69','70-79','80-89','90+'], include_lowest=True)
df_inhab_gender_prov = df_inhab.groupby(['sc_provence', 'CD_SEX', 'AGEGROUP'])['MS_POPULATION'].sum().reset_index()
df_inhab_gender_prov_cases = pd.merge(df_inhab_gender_prov, df_tot_sc.dropna(), left_on=['sc_provence', 'AGEGROUP', 'CD_SEX'], right_on=['PROVINCE', 'AGEGROUP', 'SEX'])
| sc_provence | CD_SEX | AGEGROUP | MS_POPULATION | DATE | PROVINCE | REGION | SEX | CASES | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Antwerpen | F | 0-9 | 113851 | 2020-03-05 | Antwerpen | Flanders | F | 1 |
| 1 | Antwerpen | F | 0-9 | 113851 | 2020-03-18 | Antwerpen | Flanders | F | 1 |
| 2 | Antwerpen | F | 0-9 | 113851 | 2020-03-26 | Antwerpen | Flanders | F | 1 |
| 3 | Antwerpen | F | 0-9 | 113851 | 2020-03-30 | Antwerpen | Flanders | F | 1 |
| 4 | Antwerpen | F | 0-9 | 113851 | 2020-04-03 | Antwerpen | Flanders | F | 1 |
df_plot = df_inhab_gender_prov_cases.groupby(['SEX', 'AGEGROUP', 'PROVINCE']).agg(CASES = ('CASES', 'sum'), MS_POPULATION=('MS_POPULATION', 'first')).reset_index()
df_plot
| SEX | AGEGROUP | PROVINCE | CASES | MS_POPULATION | |
|---|---|---|---|---|---|
| 0 | F | 0-9 | Antwerpen | 9 | 113851 |
| 1 | F | 0-9 | BrabantWallon | 3 | 23744 |
| 2 | F | 0-9 | Hainaut | 11 | 81075 |
| 3 | F | 0-9 | Limburg | 11 | 48102 |
| 4 | F | 0-9 | Liège | 19 | 67479 |
| ... | ... | ... | ... | ... | ... |
| 195 | M | 90+ | Luxembourg | 17 | 469 |
| 196 | M | 90+ | Namur | 27 | 827 |
| 197 | M | 90+ | OostVlaanderen | 102 | 3105 |
| 198 | M | 90+ | VlaamsBrabant | 129 | 2611 |
| 199 | M | 90+ | WestVlaanderen | 121 | 3292 |
200 rows × 5 columns
array(['Antwerpen', 'BrabantWallon', 'Hainaut', 'Limburg', 'Liège',
'Luxembourg', 'Namur', 'OostVlaanderen', 'VlaamsBrabant',
'WestVlaanderen'], dtype=object)
alt.Chart(df_plot).mark_bar().encode(x='AGEGROUP:N', y='percentage', color='SEX:N', column='PROVINCE:N')
Let's add a colorscale the makes the male blue and female number pink.
alt.Chart(df_plot).mark_bar().encode(
x='AGEGROUP:N',
y='percentage',
color=alt.Color('SEX:N', scale=color_scale, legend=None),
column='PROVINCE:N')
The graph's get to wide. Let's use faceting to make two rows.
Inspired and based on https://altair-viz.github.io/gallery/us_population_pyramid_over_time.html
#slider = alt.binding_range(min=1850, max=2000, step=10)
# select_province = alt.selection_single(name='PROVINCE', fields=['PROVINCE'],
# bind=slider, init={'PROVINCE': 'Antwerpen'})
color_scale = alt.Scale(domain=['Male', 'Female'],
range=['#1f77b4', '#e377c2'])
select_province = alt.selection_multi(fields=['PROVINCE'], bind='legend')
base = alt.Chart(df_plot).add_selection(
select_province
).transform_filter(
select_province
).transform_calculate(
gender=alt.expr.if_(alt.datum.SEX == 'M', 'Male', 'Female')
).properties(
width=250
)
left = base.transform_filter(
alt.datum.gender == 'Female'
).encode(
y=alt.Y('AGEGROUP:O', axis=None),
x=alt.X('percentage:Q', axis=alt.Axis(format='.0%'),
title='Percentage',
sort=alt.SortOrder('descending'),
),
color=alt.Color('gender:N', scale=color_scale, legend=None),
).mark_bar().properties(title='Female')
middle = base.encode(
y=alt.Y('AGEGROUP:O', axis=None),
text=alt.Text('AGEGROUP:O'),
).mark_text().properties(width=20)
right = base.transform_filter(
alt.datum.gender == 'Male'
).encode(
y=alt.Y('AGEGROUP:O', axis=None),
x=alt.X('percentage:Q', title='Percentage', axis=alt.Axis(format='.0%'),),
color=alt.Color('gender:N', scale=color_scale, legend=None)
).mark_bar().properties(title='Male')
# legend = alt.Chart(df_plot).mark_text().encode(
# y=alt.Y('PROVINCE:N', axis=None),
# text=alt.Text('PROVINCE:N'),
# color=alt.Color('PROVINCE:N', legend=alt.Legend(title="Provincie"))
# )
alt.concat(left, middle, right, spacing=5)
#legend=alt.Legend(title="Species by color")
provinces = df_plot['PROVINCE'].unique()
select_province = alt.selection_single(
name='Select', # name the selection 'Select'
fields=['PROVINCE'], # limit selection to the Major_Genre field
init={'PROVINCE': 'Antwerpen'}, # use first genre entry as initial value
bind=alt.binding_select(options=provinces) # bind to a menu of unique provence values
)
base = alt.Chart(df_plot).add_selection(
select_province
).transform_filter(
select_province
).transform_calculate(
gender=alt.expr.if_(alt.datum.SEX == 'M', 'Male', 'Female')
).properties(
width=250
)
left = base.transform_filter(
alt.datum.gender == 'Female'
).encode(
y=alt.Y('AGEGROUP:O', axis=None),
x=alt.X('percentage:Q', axis=alt.Axis(format='.0%'),
title='Percentage',
sort=alt.SortOrder('descending'),
scale=alt.Scale(domain=(0.0, 0.1), clamp=True)
),
color=alt.Color('gender:N', scale=color_scale, legend=None),
tooltip=[alt.Tooltip('percentage', format='.1%')]
).mark_bar().properties(title='Female')
middle = base.encode(
y=alt.Y('AGEGROUP:O', axis=None),
text=alt.Text('AGEGROUP:O'),
).mark_text().properties(width=20)
right = base.transform_filter(
alt.datum.gender == 'Male'
).encode(
y=alt.Y('AGEGROUP:O', axis=None),
x=alt.X('percentage:Q', title='Percentage', axis=alt.Axis(format='.1%'), scale=alt.Scale(domain=(0.0, 0.1), clamp=True)),
color=alt.Color('gender:N', scale=color_scale, legend=None),
tooltip=[alt.Tooltip('percentage', format='.1%')]
).mark_bar().properties(title='Male')
alt.concat(left, middle, right, spacing=5).properties(title='Percentage of covid-19 cases per province, gender and age grup in Belgium')
Mortality
# https://epistat.wiv-isp.be/covid/
# Dataset of mortality by date, age, sex, and region
df_dead_sc = pd.read_csv('https://epistat.sciensano.be/Data/COVID19BE_MORT.csv')
| DATE | REGION | AGEGROUP | SEX | DEATHS | |
|---|---|---|---|---|---|
| 0 | 2020-03-10 | Brussels | 85+ | F | 1 |
| 1 | 2020-03-11 | Flanders | 85+ | F | 1 |
| 2 | 2020-03-11 | Brussels | 75-84 | M | 1 |
| 3 | 2020-03-11 | Brussels | 85+ | F | 1 |
| 4 | 2020-03-12 | Brussels | 75-84 | M | 1 |
Wallonia 291
Flanders 275
Brussels 271
Name: REGION, dtype: int64
85+ 223
75-84 205
65-74 179
45-64 132
25-44 19
0-24 1
Name: AGEGROUP, dtype: int64
df_inhab['AGEGROUP_sc'] =pd.cut(df_inhab['CD_AGE'], bins=[0,24,44,64,74,84,200], labels=['0-24','25-44','45-64','65-74','75-84','85+'], include_lowest=True)
| lowest_age | highest_age | |
|---|---|---|
| AGEGROUP_sc | ||
| 0-24 | 0 | 24 |
| 25-44 | 25 | 44 |
| 45-64 | 45 | 64 |
| 65-74 | 65 | 74 |
| 75-84 | 75 | 84 |
| 85+ | 85 | 110 |
| CD_REFNIS | TX_DESCR_NL | TX_DESCR_FR | CD_DSTR_REFNIS | TX_ADM_DSTR_DESCR_NL | TX_ADM_DSTR_DESCR_FR | CD_PROV_REFNIS | TX_PROV_DESCR_NL | TX_PROV_DESCR_FR | CD_RGN_REFNIS | TX_RGN_DESCR_NL | TX_RGN_DESCR_FR | CD_SEX | CD_NATLTY | TX_NATLTY_NL | TX_NATLTY_FR | CD_CIV_STS | TX_CIV_STS_NL | TX_CIV_STS_FR | CD_AGE | MS_POPULATION | sc_provence | AGEGROUP | AGEGROUP_sc | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 11001 | Aartselaar | Aartselaar | 11000 | Arrondissement Antwerpen | Arrondissement d’Anvers | 10000.0 | Provincie Antwerpen | Province d’Anvers | 2000 | Vlaams Gewest | Région flamande | F | BEL | Belgen | Belges | 4 | Gescheiden | Divorcé | 69 | 11 | Antwerpen | 60-69 | 65-74 |
| 1 | 11001 | Aartselaar | Aartselaar | 11000 | Arrondissement Antwerpen | Arrondissement d’Anvers | 10000.0 | Provincie Antwerpen | Province d’Anvers | 2000 | Vlaams Gewest | Région flamande | F | BEL | Belgen | Belges | 4 | Gescheiden | Divorcé | 80 | 3 | Antwerpen | 70-79 | 75-84 |
| 2 | 11001 | Aartselaar | Aartselaar | 11000 | Arrondissement Antwerpen | Arrondissement d’Anvers | 10000.0 | Provincie Antwerpen | Province d’Anvers | 2000 | Vlaams Gewest | Région flamande | M | BEL | Belgen | Belges | 4 | Gescheiden | Divorcé | 30 | 2 | Antwerpen | 20-29 | 25-44 |
| 3 | 11001 | Aartselaar | Aartselaar | 11000 | Arrondissement Antwerpen | Arrondissement d’Anvers | 10000.0 | Provincie Antwerpen | Province d’Anvers | 2000 | Vlaams Gewest | Région flamande | F | BEL | Belgen | Belges | 4 | Gescheiden | Divorcé | 48 | 26 | Antwerpen | 40-49 | 45-64 |
| 4 | 11001 | Aartselaar | Aartselaar | 11000 | Arrondissement Antwerpen | Arrondissement d’Anvers | 10000.0 | Provincie Antwerpen | Province d’Anvers | 2000 | Vlaams Gewest | Région flamande | F | BEL | Belgen | Belges | 4 | Gescheiden | Divorcé | 76 | 2 | Antwerpen | 70-79 | 75-84 |
array(['Brussels', 'Flanders', 'Wallonia'], dtype=object)
Vlaams Gewest 242865
Waals Gewest 199003
Brussels Hoofdstedelijk Gewest 21513
Name: TX_RGN_DESCR_NL, dtype: int64
df_inhab_gender_prov = df_inhab.groupby(['TX_RGN_DESCR_NL', 'CD_SEX', 'AGEGROUP_sc'])['MS_POPULATION'].sum().reset_index()
region_sc_to_region_inhad = {'Flanders':'Vlaams Gewest', 'Wallonia':'Waals Gewest', 'Brussels':'Brussels Hoofdstedelijk Gewest'}
TX_RGN_DESCR_NL AGEGROUP SEX
Brussels Hoofdstedelijk Gewest 25-44 F 1
M 4
45-64 F 21
M 43
65-74 F 42
M 71
75-84 F 128
M 170
85+ F 270
M 186
Vlaams Gewest 0-24 F 1
25-44 F 2
M 3
45-64 F 27
M 63
65-74 F 67
M 130
75-84 F 199
M 335
85+ F 232
M 309
Waals Gewest 25-44 F 5
M 4
45-64 F 41
M 89
65-74 F 98
M 186
75-84 F 290
M 300
85+ F 704
M 421
Name: DEATHS, dtype: int64
df_dead_sc_region_agegroup_gender = df_dead_sc.groupby(['TX_RGN_DESCR_NL', 'AGEGROUP', 'SEX'])['DEATHS'].sum().reset_index()
df_inhab_gender_prov_deaths = pd.merge(df_inhab_gender_prov, df_dead_sc_region_agegroup_gender, left_on=['TX_RGN_DESCR_NL', 'AGEGROUP_sc', 'CD_SEX'], right_on=['TX_RGN_DESCR_NL', 'AGEGROUP', 'SEX'])
9077403
4442
| TX_RGN_DESCR_NL | CD_SEX | AGEGROUP_sc | MS_POPULATION | AGEGROUP | SEX | DEATHS | |
|---|---|---|---|---|---|---|---|
| 0 | Brussels Hoofdstedelijk Gewest | F | 25-44 | 197579 | 25-44 | F | 1 |
| 1 | Brussels Hoofdstedelijk Gewest | F | 45-64 | 137628 | 45-64 | F | 21 |
| 2 | Brussels Hoofdstedelijk Gewest | F | 65-74 | 45214 | 65-74 | F | 42 |
| 3 | Brussels Hoofdstedelijk Gewest | F | 75-84 | 30059 | 75-84 | F | 128 |
| 4 | Brussels Hoofdstedelijk Gewest | F | 85+ | 18811 | 85+ | F | 270 |
| 5 | Brussels Hoofdstedelijk Gewest | M | 25-44 | 194988 | 25-44 | M | 4 |
| 6 | Brussels Hoofdstedelijk Gewest | M | 45-64 | 140348 | 45-64 | M | 43 |
| 7 | Brussels Hoofdstedelijk Gewest | M | 65-74 | 36698 | 65-74 | M | 71 |
| 8 | Brussels Hoofdstedelijk Gewest | M | 75-84 | 19969 | 75-84 | M | 170 |
| 9 | Brussels Hoofdstedelijk Gewest | M | 85+ | 7918 | 85+ | M | 186 |
| 10 | Vlaams Gewest | F | 0-24 | 874891 | 0-24 | F | 1 |
| 11 | Vlaams Gewest | F | 25-44 | 820036 | 25-44 | F | 2 |
| 12 | Vlaams Gewest | F | 45-64 | 901554 | 45-64 | F | 27 |
| 13 | Vlaams Gewest | F | 65-74 | 353925 | 65-74 | F | 67 |
| 14 | Vlaams Gewest | F | 75-84 | 245981 | 75-84 | F | 199 |
| 15 | Vlaams Gewest | F | 85+ | 132649 | 85+ | F | 232 |
| 16 | Vlaams Gewest | M | 25-44 | 827281 | 25-44 | M | 3 |
| 17 | Vlaams Gewest | M | 45-64 | 917008 | 45-64 | M | 63 |
| 18 | Vlaams Gewest | M | 65-74 | 336242 | 65-74 | M | 130 |
| 19 | Vlaams Gewest | M | 75-84 | 193576 | 75-84 | M | 335 |
| 20 | Vlaams Gewest | M | 85+ | 69678 | 85+ | M | 309 |
| 21 | Waals Gewest | F | 25-44 | 457356 | 25-44 | F | 5 |
| 22 | Waals Gewest | F | 45-64 | 496668 | 45-64 | F | 41 |
| 23 | Waals Gewest | F | 65-74 | 199422 | 65-74 | F | 98 |
| 24 | Waals Gewest | F | 75-84 | 118224 | 75-84 | F | 290 |
| 25 | Waals Gewest | F | 85+ | 68502 | 85+ | F | 704 |
| 26 | Waals Gewest | M | 25-44 | 459444 | 25-44 | M | 4 |
| 27 | Waals Gewest | M | 45-64 | 487322 | 45-64 | M | 89 |
| 28 | Waals Gewest | M | 65-74 | 175508 | 65-74 | M | 186 |
| 29 | Waals Gewest | M | 75-84 | 82876 | 75-84 | M | 300 |
| 30 | Waals Gewest | M | 85+ | 30048 | 85+ | M | 421 |
df_inhab_gender_prov_deaths['percentage'] = df_inhab_gender_prov_deaths['DEATHS']/df_inhab_gender_prov_deaths['MS_POPULATION']
regions = df_plot['TX_RGN_DESCR_NL'].unique()
select_province = alt.selection_single(
name='Select', # name the selection 'Select'
fields=['TX_RGN_DESCR_NL'], # limit selection to the Major_Genre field
init={'TX_RGN_DESCR_NL': 'Vlaams Gewest'}, # use first genre entry as initial value
bind=alt.binding_select(options=regions) # bind to a menu of unique provence values
)
base = alt.Chart(df_plot).add_selection(
select_province
).transform_filter(
select_province
).transform_calculate(
gender=alt.expr.if_(alt.datum.SEX == 'M', 'Male', 'Female')
).properties(
width=250
)
left = base.transform_filter(
alt.datum.gender == 'Female'
).encode(
y=alt.Y('AGEGROUP:O', axis=None),
x=alt.X('percentage:Q', axis=alt.Axis(format='.2%'),
title='Percentage',
sort=alt.SortOrder('descending'),
# scale=alt.Scale(domain=(0.0, 0.02), clamp=True)
),
color=alt.Color('gender:N', scale=color_scale, legend=None),
tooltip=[alt.Tooltip('percentage', format='.2%')]
).mark_bar().properties(title='Female')
middle = base.encode(
y=alt.Y('AGEGROUP:O', axis=None),
text=alt.Text('AGEGROUP:O'),
).mark_text().properties(width=20)
right = base.transform_filter(
alt.datum.gender == 'Male'
).encode(
y=alt.Y('AGEGROUP:O', axis=None),
# x=alt.X('percentage:Q', title='Percentage', axis=alt.Axis(format='.2%'), scale=alt.Scale(domain=(0.0, 0.02), clamp=True)),
x=alt.X('percentage:Q', title='Percentage', axis=alt.Axis(format='.2%')),
color=alt.Color('gender:N', scale=color_scale, legend=None),
tooltip=[alt.Tooltip('percentage', format='.2%')]
).mark_bar().properties(title='Male')
alt.concat(left, middle, right, spacing=5).properties(title='Percentage of covid-19 deaths per province, gender and age group relative to number of inhabitants in Belgium')
Daily covid-19 Deaths compared to average deaths the last 10 years
"In this blogpost we try to get an idea of how many extra deaths we have in Belgium due to covid-19 compared to the average we had the last 10 years."
The number of deadths per day from 2008 until 2018 can obtained from Statbel, the Belgium federal bureau of statistics:
df = pd.read_excel('https://statbel.fgov.be/sites/default/files/files/opendata/bevolking/TF_DEATHS.xlsx') # , skiprows=5, sheet_name=sheetnames
| DT_DATE | MS_NUM_DEATHS | |
|---|---|---|
| 0 | 2008-01-01 | 342 |
| 1 | 2008-01-02 | 348 |
| 2 | 2008-01-03 | 340 |
| 3 | 2008-01-04 | 349 |
| 4 | 2008-01-05 | 348 |
# Let's make a quick plot
alt.Chart(df_plot).mark_line().encode(x='Dag', y='MS_NUM_DEATHS').properties(width=600)
The John Hopkings University CSSE keeps track of the number of covid-19 deadths per day and country in a github repository: https://github.com/CSSEGISandData/COVID-19. We can easily obtain this data by reading it from github and filter out the cases for Belgium.
deaths_url = 'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_deaths_global.csv'
deaths = pd.read_csv(deaths_url, sep=',')
Filter out Belgium
Inspect how the data is stored
| Province/State | Country/Region | Lat | Long | 1/22/20 | 1/23/20 | 1/24/20 | 1/25/20 | 1/26/20 | 1/27/20 | ... | 4/9/20 | 4/10/20 | 4/11/20 | 4/12/20 | 4/13/20 | 4/14/20 | 4/15/20 | 4/16/20 | 4/17/20 | 4/18/20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 23 | NaN | Belgium | 50.8333 | 4.0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 2523 | 3019 | 3346 | 3600 | 3903 | 4157 | 4440 | 4857 | 5163 | 5453 |
1 rows × 92 columns
Create dateframe for plotting
df_deaths = pd.DataFrame(data={'Datum':pd.to_datetime(deaths_be.columns[4:]), 'Overlijdens':deaths_be.iloc[0].values[4:]})
Check for Nan's
0
We need to do some type convertions. We cast 'Overlijdens' to integer. Next, we add the number of the day.
df_deaths['Overlijdens'] = df_deaths['Overlijdens'].astype(int)
df_deaths['Dag'] = df_deaths['Datum'].dt.dayofyear
Plot the data:
Calculate the day-by-day change
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 88 entries, 0 to 87
Data columns (total 4 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Datum 88 non-null datetime64[ns]
1 Overlijdens 88 non-null int32
2 Dag 88 non-null int64
3 Nieuwe covid-19 Sterfgevallen 87 non-null float64
dtypes: datetime64[ns](1), float64(1), int32(1), int64(1)
memory usage: 2.5 KB
Plot covid-19 deaths in Belgium according to JHU CSSE. The plot shows a tooltip if you hover over the points.
dead_covid= alt.Chart(df_deaths).mark_line(point=True).encode(
x=alt.X('Dag',scale=alt.Scale(domain=(1, 110), clamp=True)),
y='Nieuwe covid-19 Sterfgevallen',
color=alt.ColorValue('red'),
tooltip=['Dag', 'Nieuwe covid-19 Sterfgevallen'])
dead_covid
Now we add average deaths per day in the last 10 year to the plot.
Take quick look to the datatable:
| DT_DATE | MS_NUM_DEATHS | Jaar | Dag | |
|---|---|---|---|---|
| 0 | 2008-01-01 | 342 | 2008 | 1 |
| 1 | 2008-01-02 | 348 | 2008 | 2 |
| 2 | 2008-01-03 | 340 | 2008 | 3 |
| 3 | 2008-01-04 | 349 | 2008 | 4 |
| 4 | 2008-01-05 | 348 | 2008 | 5 |
The column 'DT_DATE' is a string. We convert it to a datatime so we can add it to the tooltip.
Now we are prepared to make the final graph. We use the Altair mark_errorband(extend='ci') to bootstrap 95% confidence band around the average number of deaths per day.
line = alt.Chart(df).mark_line().encode(
x=alt.X('Dag', scale=alt.Scale(
domain=(1, 120),
clamp=True
)),
y='mean(MS_NUM_DEATHS)'
)
# Bootstrapped 95% confidence interval
band = alt.Chart(df).mark_errorband(extent='ci').encode(
x=alt.X('Dag', scale=alt.Scale(domain=(1, 120), clamp=True)),
y=alt.Y('MS_NUM_DEATHS', title='Overlijdens per dag'),
)
dead_covid= alt.Chart(df_deaths).mark_line(point=True).encode(
x=alt.X('Dag',scale=alt.Scale(domain=(1, 120), clamp=True)),
y='Nieuwe covid-19 Sterfgevallen',
color=alt.ColorValue('red'),
tooltip=['Dag', 'Nieuwe covid-19 Sterfgevallen', 'Datum']
)
(band + line + dead_covid).properties(width=1024, title='Gemiddeld aantal overlijdens over 10 jaar versus overlijdens door covid-19 in Belgie')
Source date from sciensano
In this section, we compare the graph obtained with data obtained from sciensano.
| DATE | REGION | AGEGROUP | SEX | DEATHS | |
|---|---|---|---|---|---|
| 0 | 2020-03-10 | Brussels | 85+ | F | 1 |
| 1 | 2020-03-11 | Flanders | 85+ | F | 1 |
| 2 | 2020-03-11 | Brussels | 75-84 | M | 1 |
| 3 | 2020-03-11 | Brussels | 85+ | F | 1 |
| 4 | 2020-03-12 | Brussels | 75-84 | M | 1 |
df_dead_day = df_sc.groupby('DATE')['DEATHS'].sum().reset_index()
df_dead_day['Datum'] = pd.to_datetime(df_dead_day['DATE'])
df_dead_day['Dag'] = df_dead_day['Datum'].dt.dayofyear
line = alt.Chart(df).mark_line().encode(
x=alt.X('Dag', title='Dag van het jaar', scale=alt.Scale(
domain=(1, 120),
clamp=True
)),
y='mean(MS_NUM_DEATHS)'
)
# Bootstrapped 95% confidence interval
band = alt.Chart(df).mark_errorband(extent='ci').encode(
x=alt.X('Dag', scale=alt.Scale(domain=(1, 120), clamp=True)),
y=alt.Y('MS_NUM_DEATHS', title='Overlijdens per dag'),
)
dead_covid= alt.Chart(df_dead_day).mark_line(point=True).encode(
x=alt.X('Dag',scale=alt.Scale(domain=(1, 120), clamp=True)),
y='DEATHS',
color=alt.ColorValue('red'),
tooltip=['Dag', 'DEATHS', 'Datum']
)
(band + line + dead_covid).properties(width=750, title='Gemiddeld aantal overlijdens over 10 jaar versus overlijdens door covid-19 in Belgie')
Obviously, data form 16-17-18 April 2020 is not final yet. Also, the amounts are smaller then those from JHU.
Obtain more detail (for another blogpost...)
| DATE | PROVINCE | REGION | AGEGROUP | SEX | CASES | |
|---|---|---|---|---|---|---|
| 0 | 2020-03-01 | Brussels | Brussels | 10-19 | M | 1 |
| 1 | 2020-03-01 | Brussels | Brussels | 10-19 | F | 1 |
| 2 | 2020-03-01 | Brussels | Brussels | 20-29 | M | 1 |
| 3 | 2020-03-01 | Brussels | Brussels | 30-39 | F | 1 |
| 4 | 2020-03-01 | Brussels | Brussels | 40-49 | F | 1 |
| ... | ... | ... | ... | ... | ... | ... |
| 6875 | NaN | OostVlaanderen | Flanders | NaN | F | 4 |
| 6876 | NaN | VlaamsBrabant | Flanders | 40-49 | M | 3 |
| 6877 | NaN | VlaamsBrabant | Flanders | 40-49 | F | 2 |
| 6878 | NaN | VlaamsBrabant | Flanders | 50-59 | M | 1 |
| 6879 | NaN | WestVlaanderen | Flanders | 50-59 | M | 3 |
6880 rows × 6 columns
We know that there are a lot of reional differences:
| DATE | PROVINCE | CASES | |
|---|---|---|---|
| 0 | 2020-03-01 | Brussels | 6 |
| 1 | 2020-03-01 | Limburg | 1 |
| 2 | 2020-03-01 | Liège | 2 |
| 3 | 2020-03-01 | OostVlaanderen | 1 |
| 4 | 2020-03-01 | VlaamsBrabant | 6 |
| ... | ... | ... | ... |
| 505 | 2020-04-17 | OostVlaanderen | 44 |
| 506 | 2020-04-17 | VlaamsBrabant | 42 |
| 507 | 2020-04-17 | WestVlaanderen | 30 |
| 508 | 2020-04-18 | Brussels | 1 |
| 509 | 2020-04-18 | Hainaut | 1 |
510 rows × 3 columns
base = alt.Chart(df_plot, title='Number of cases in Belgium per day and province').mark_line(point=True).encode(
x=alt.X('DATE:T', title='Datum'),
y=alt.Y('CASES', title='Cases per day'),
color='PROVINCE',
tooltip=['DATE', 'CASES', 'PROVINCE']
).properties(width=600)
base
From the above graph we see a much lower number of cases in Luxembourg, Namur, Waals Brabant.
'pwd' is not recognized as an internal or external command,
operable program or batch file.
Volume in drive C is Windows
Volume Serial Number is 7808-E933
Directory of C:\Users\lnh6dt5\AppData\Local\Temp\Mxt121\tmp\home_lnh6dt5\blog\_notebooks
19/04/2020 14:14 <DIR> .
19/04/2020 14:14 <DIR> ..
19/04/2020 10:37 <DIR> .ipynb_checkpoints
19/04/2020 10:17 23.473 2020-01-28-Altair.ipynb
19/04/2020 10:34 9.228 2020-01-29-bullet-chart-altair.ipynb
19/04/2020 10:26 41.041 2020-02-15-breakins.ipynb
19/04/2020 09:43 30.573 2020-02-20-test.ipynb
19/04/2020 09:49 1.047 2020-04-18-first-test.ipynb
19/04/2020 14:14 1.237.674 2020-04-19-deads-last-ten-year-vs-covid.ipynb
19/04/2020 09:43 <DIR> my_icons
19/04/2020 09:43 771 README.md
7 File(s) 1.343.807 bytes
4 Dir(s) 89.905.336.320 bytes free
First test post
Testing a simple notebook for publishing with fastpages
Evolution of burglary in Leuven. Is the trend downwards ?
Evolution of burglary in Leuven. Is the trend downwards ?
The local police shared a graph with the number of break-ins in Leuven per year. The article shows a graph with a downwards trendline. Can we conclude that the number of breakins is showing a downward trend based on those numbers? Let's construct a dataframe with the data from the graph.
import numpy as np
import pandas as pd
import altair as alt
df = pd.DataFrame({'year_int':[y for y in range(2006, 2020)],
'breakins':[1133,834,953,891,1006,1218,992,1079,1266,1112,713,669,730,644]})
df['year'] = pd.to_datetime(df['year_int'], format='%Y')
points = alt.Chart(df).mark_line(point=True).encode(
x='year', y='breakins', tooltip='breakins'
)
points + points.transform_regression('year', 'breakins').mark_line(
color='green'
).properties(
title='Regression trend on the number breakins per year in Leuven'
)
The article claims that the number of breakins stabilizes the last years. Let's perform a local regression to check that.
# https://opendatascience.com/local-regression-in-python
# Loess: https://gist.github.com/AllenDowney/818f6153ef316aee80467c51faee80f8
points + points.transform_loess('year', 'breakins').mark_line(
color='green'
).properties(
title='Local regression trend on the number breakins per year in Leuven'
)
But what about the trend line? Are we sure the trend is negative ? Bring in the code based on the blogpost The hacker's guide to uncertainty estimates to estimate the uncertainty.:
# Code from: https://erikbern.com/2018/10/08/the-hackers-guide-to-uncertainty-estimates.html
import scipy.optimize
import random
def model(xs, k, m):
return k * xs + m
def neg_log_likelihood(tup, xs, ys):
# Since sigma > 0, we use use log(sigma) as the parameter instead.
# That way we have an unconstrained problem.
k, m, log_sigma = tup
sigma = np.exp(log_sigma)
delta = model(xs, k, m) - ys
return len(xs)/2*np.log(2*np.pi*sigma**2) + \
np.dot(delta, delta) / (2*sigma**2)
def confidence_bands(xs, ys, nr_bootstrap):
curves = []
xys = list(zip(xs, ys))
for i in range(nr_bootstrap):
# sample with replacement
bootstrap = [random.choice(xys) for _ in xys]
xs_bootstrap = np.array([x for x, y in bootstrap])
ys_bootstrap = np.array([y for x, y in bootstrap])
k_hat, m_hat, log_sigma_hat = scipy.optimize.minimize(
neg_log_likelihood, (0, 0, 0), args=(xs_bootstrap, ys_bootstrap)
).x
curves.append(
model(xs, k_hat, m_hat) +
# Note what's going on here: we're _adding_ the random term
# to the predictions!
np.exp(log_sigma_hat) * np.random.normal(size=xs.shape)
)
lo, hi = np.percentile(curves, (2.5, 97.5), axis=0)
return lo, hi
# Make a plot with a confidence band
df['lo'], df['hi'] = confidence_bands(df.index, df['breakins'], 100)
ci = alt.Chart(df).mark_area().encode(
x=alt.X('year:T', title=''),
y=alt.Y('lo:Q'),
y2=alt.Y2('hi:Q', title=''),
color=alt.value('lightblue'),
opacity=alt.value(0.6)
)
chart = alt.Chart(df).mark_line(point=True).encode(
x='year', y='breakins', tooltip='breakins'
)
ci + chart + chart.transform_regression('year', 'breakins').mark_line(
color='red'
).properties(
title='95% Confidence band of the number of breakins per year in Leuven'
)
On the above chart, we see that a possitive trend might be possible as well.
Linear regression
Let's perform a linear regression with statsmodel to calculate the confidence interval on the slope of the regression line.
Intercept 1096.314286
index -23.169231
dtype: float64
The most likely slope of the trend line is 23.17 breakins per year. But how sure are we that the trend is heading down ?
C:\Users\lnh6dt5\AppData\Local\Continuum\anaconda3\lib\site-packages\scipy\stats\stats.py:1535: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=14
"anyway, n=%i" % int(n))
| Dep. Variable: | breakins | R-squared: | 0.223 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.159 |
| Method: | Least Squares | F-statistic: | 3.451 |
| Date: | Sun, 19 Apr 2020 | Prob (F-statistic): | 0.0879 |
| Time: | 10:26:45 | Log-Likelihood: | -92.105 |
| No. Observations: | 14 | AIC: | 188.2 |
| Df Residuals: | 12 | BIC: | 189.5 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 1096.3143 | 95.396 | 11.492 | 0.000 | 888.465 | 1304.164 |
| index | -23.1692 | 12.472 | -1.858 | 0.088 | -50.344 | 4.006 |
| Omnibus: | 1.503 | Durbin-Watson: | 1.035 |
|---|---|---|---|
| Prob(Omnibus): | 0.472 | Jarque-Bera (JB): | 1.196 |
| Skew: | 0.577 | Prob(JB): | 0.550 |
| Kurtosis: | 2.153 | Cond. No. | 14.7 |
Warnings:[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
The analysis reveals that the slope of the best fitting regression line is 23 breakins less per year. However, the confidence interval of the trend is between -50.344 and 4.006. Also the p)value of the regression coefficient is 0.088. Meaning we have eight percent chance that the negative trend is by accident. Hence, based on the current data we are not 95% percent sure the trend is downwards. Hence we can not conclude, based on this data, that there is a negative trend. This corresponds with the width of the 95% certainty band drawn that allows for an upward trend line:
| 0 | 1 | |
|---|---|---|
| Intercept | 888.464586 | 1304.163986 |
| index | -50.344351 | 4.005889 |
y_low = results.params['Intercept'] # ?ost likely value of the intercept
y_high = results.params['Intercept'] + results.conf_int()[1]['index'] * df.shape[0] # Value of upward trend for the last year
df_upward_trend = pd.DataFrame({'year':[df['year'].min(), df['year'].max()],
'breakins':[y_low, y_high]})
possible_upwards_trend = alt.Chart(df_upward_trend).mark_line(
color='green',
strokeDash=[10,10]
).encode(
x='year:T',
y=alt.Y('breakins:Q',
title='Number of breakins per year')
)
points = alt.Chart(df).mark_line(point=True).encode(x='year', y='breakins', tooltip='breakins')
(ci + points + points.transform_regression('year', 'breakins').mark_line(color='red')
+ possible_upwards_trend).properties(
title='Trend analysis on the number of breakins per year in Leuven, Belgium'
)
In the above graph, we see that a slight positive trend (green dashed line) is in the 95% confidence band on the regression coefficient. We are not sure that the trend on the number of breakins is downwards.
Bullet chart in python Altair
How to make bullet charts with Altair
In the article "Bullet Charts - What Is It And How To Use It" I learned about Bullet charts. It's a specific kind of barchart that must convey the state of a measure or KPI. The goal is to see in a glance if the target is met. Here is an example bullet chart from the article:
# This causes issues to:
# from IPython.display import Image
# Image('https://jscharting.com/blog/bullet-charts/images/bullet_components.png')
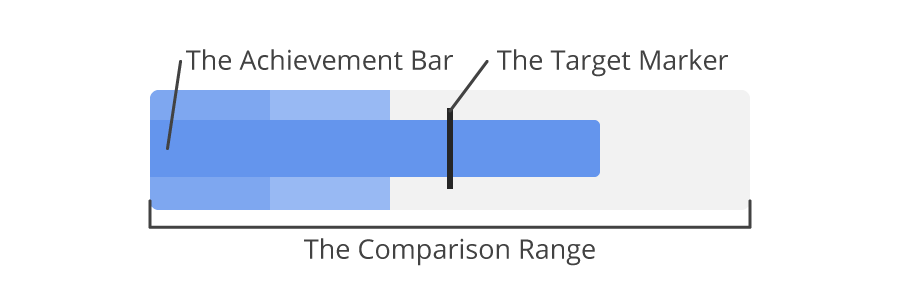
# <img src="https://jscharting.com/blog/bullet-charts/images/bullet_components.png" alt="Bullet chart" style="width: 200px;"/>
Below is some Python code that generates bullets graphs using the Altair library.
import altair as alt
import pandas as pd
df = pd.DataFrame.from_records([
{"title":"Revenue","subtitle":"US$, in thousands","ranges":[150,225,300],"measures":[220,270],"markers":[250]},
{"title":"Profit","subtitle":"%","ranges":[20,25,30],"measures":[21,23],"markers":[26]},
{"title":"Order Size","subtitle":"US$, average","ranges":[350,500,600],"measures":[100,320],"markers":[550]},
{"title":"New Customers","subtitle":"count","ranges":[1400,2000,2500],"measures":[1000,1650],"markers":[2100]},
{"title":"Satisfaction","subtitle":"out of 5","ranges":[3.5,4.25,5],"measures":[3.2,4.7],"markers":[4.4]}
])
alt.layer(
alt.Chart().mark_bar(color='#eee').encode(alt.X("ranges[2]:Q", scale=alt.Scale(nice=False), title=None)),
alt.Chart().mark_bar(color='#ddd').encode(x="ranges[1]:Q"),
alt.Chart().mark_bar(color='#bbb').encode(x="ranges[0]:Q"),
alt.Chart().mark_bar(color='steelblue', size=10).encode(x='measures[0]:Q'),
alt.Chart().mark_tick(color='black', size=12).encode(x='markers[0]:Q'),
data=df
).facet(
row=alt.Row("title:O", title='')
).resolve_scale(
x='independent'
)